上篇文章我们探讨了内约束的3个修饰符号（CZ,CZR, SIM）。内约束强调的是公差带和公差带之间必须保持某个方位关系，其本质目的是为了控制被测特征与被测特征之间的相对方位关系。

本期文章我们来继续讨论内外约束。本期文章将阐述以下的两个章节。

     3.外约束和内外约束的关系

     4.内外约束的应用案例

我们先来看看外约束和内约束之间的关系。

3. 外约束和内外约束的关系

说起内约束，有好奇的小伙伴马上就会问，那有没有外约束呢？

当然有！根据我们的鸟笼模型，晾衣杆对鸟笼的约束就属于外约束。

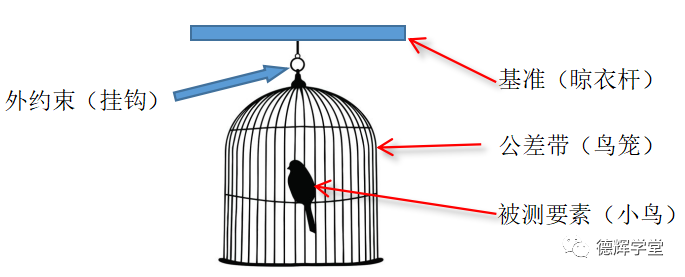
图19 来自基准的外约束

对于外约束我们再熟悉不过的，所有带基准的几何公差都存在外约束，而这些外约束都来自基准。

内约束强调的是公差带和公差带之间的关系，属于人民的内部矛盾，而外约束，是强调公差带和基准（其它特征）之间的关系，属于人民的外部矛盾。

废话少说，举个例子吧，见图20。

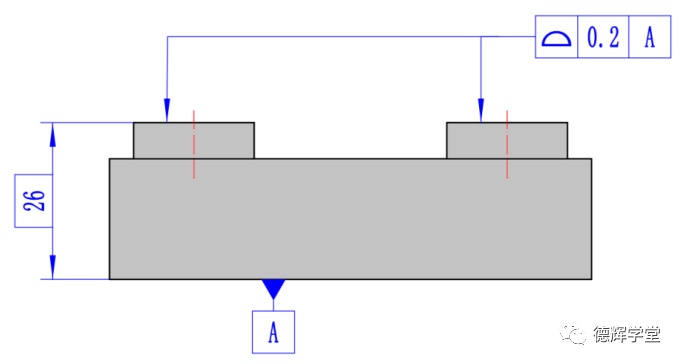
图20 带基准的轮廓度

     图20的标注，要求宽度为0.2的红色的轮廓度公差带必须和基准A保持理想的方位关系。见图21，即要求公差带A和公差带B不仅仅要和基准A绝对平行（方向关系），还要和基准A保持绝对的26的距离（位置关系）。

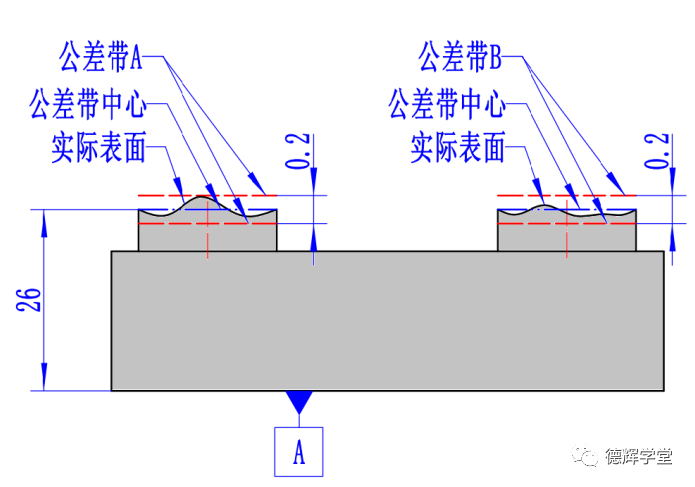
图21 受外约束的公差带

我们强调过，所有带基准的几何公差都存在外约束，因为公差带必须要和基准这个外部特征保持某种关系（要么方向，要么位置，或兼而有之）。

接下来我们再来讨论一下外约束和内约束之间的关系。

外约束能控制公差带的相对关系吗？即外约束能实现内约束的功能吗？

就那图21来说，公差带A和公差带B都必须和基准A保持理想的方位关系。我们发现，最终的结果是，公差带A和公差带B相互之间的位置关系也是理想的，即和公差带A和公差带B两公差带之间一定是“对齐”的。

就图20要求而言，外约束是间接具备内约束的功能，即能够控制公差带相互之间的方位关系。这个应该好理解，相当于我们把每个鸟笼“焊死”在晾衣杆上，那么鸟笼和鸟笼之间的关系也就定死了。见图22。

图22 外约束控制公差带相对关系

我们再来看一个案例，见图23和图24。

图23 位置度的标注

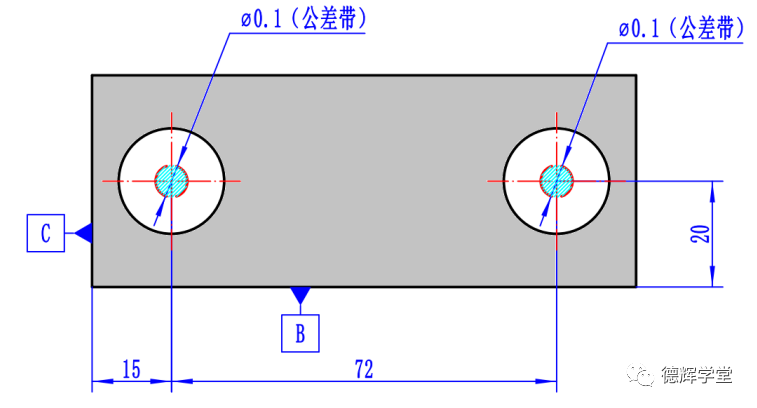
图24 受外约束的公差带

图23中位置度公差带必须要和基准系ABC保持理想的方位关系，所以，公差带受到了来自基准系的外约束。显然根据基准系的特点可知，公差带的6个自由度全部被基准系锁死，即基准系约束了图24中两个公差带所有的方向和位置。

既然两个公差带所有的自由度被外约束锁死了，那么这两个公差带的相对关系也被锁死了。所以图22中的鸟笼模型，外约束也具备内约束的功能，控制公差带和公差带之间的相互关系。

在图23中，就对零件的实际要求而言，满足以下关系：

尽管如此，我们还是要强调，在上面的标注中，设计者的真实意图其实是不一样的。左边标注表示要求特征各自的公差带必须要和基准直接保持方位关系，而右边标注则要求特征组公差带内部首先要保持方位关系，再去和基准保持理想的方位关系。

需要注意的是，外约束并不总是具备内约束的功能。

如果，我们不是“焊死”鸟笼，而是将两个鸟笼分别“挂”在晾衣杆上（即鸟笼可以在晾衣杆上滑来滑去）。我们很快就会发现，鸟笼在和晾衣杆保持约束关系的前提下，还会出现以下情况:

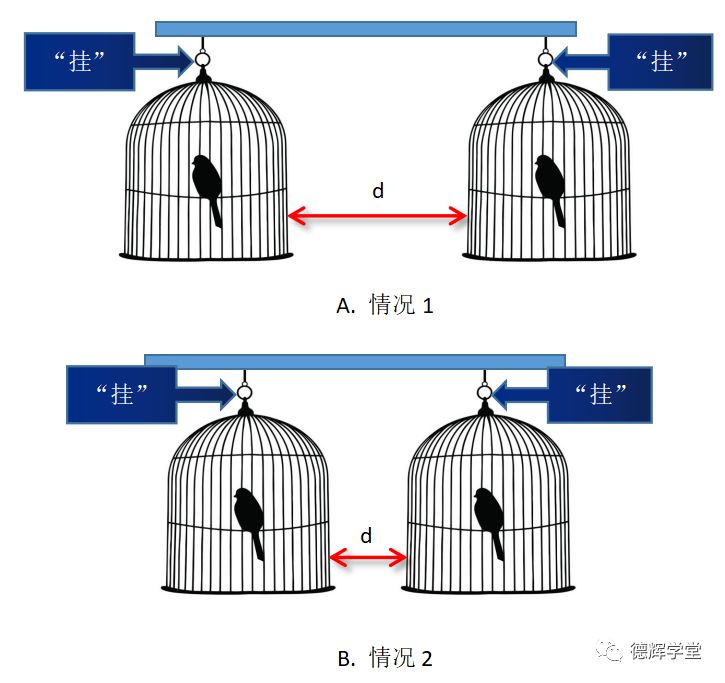
图25 鸟笼之间的相对关系d不能被控制

从图25中可以看出，如果只有外约束，而作为公差带的鸟笼还剩有自由度时，鸟笼和鸟笼之间的相对关系d则不能被控制，因为两个鸟笼各自都可以在晾衣杆上滑来滑去，相对距离d则不能保证。

图25只是比方，基于同样的逻辑，我们再来看看现实中的情况。

     如果将图23中的C基准去掉，如图26。

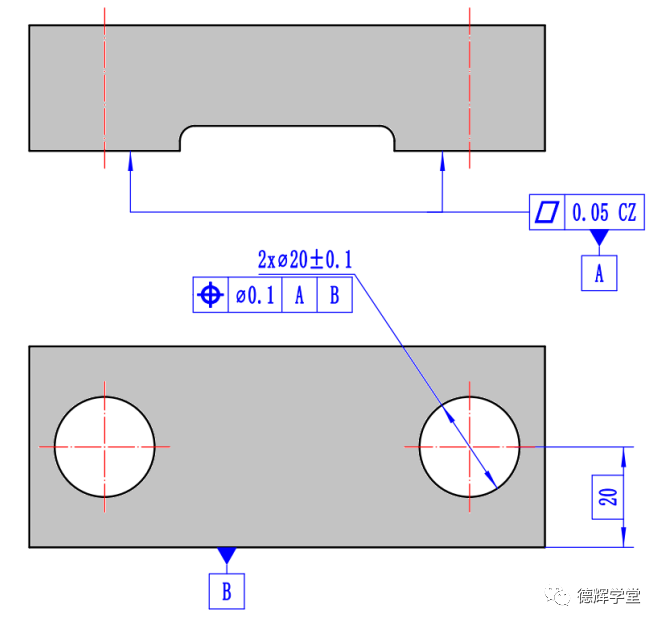
图26 少一个基准的位置度

图26中的位置度，同样要求直径为Φ0.1的公差带必须和基准系AB保持理想的方位关系，注意，因为这里没有CZ, 根据最新的ISO5458:2018, 此时的公差带只有外约束，没有内约束。

啥意思呢？即要求左右两个孔的公差带各自必须和基准系AB保持理想的方位关系，相互之间则不需要保持任何关系。见图27。

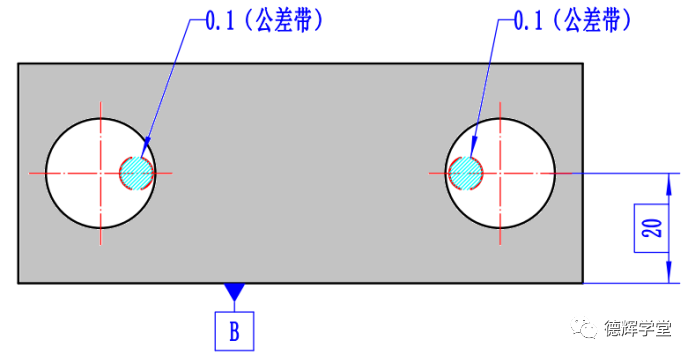
图27 只有外约束没有内约束

因为只有外约束，没有内约束，所以公差带只需要和基准系保持理想的方位关系，即两个直径为Φ0.1的公差带，各自必须和基准A理想垂直，和基准B的距离是20即可。因为基准系中缺少基准C，公差带还有一个左右飘的自由度没人管，所以两个公差带可以左右任意移动。

又因为没有内约束（缺少相应的修饰符号），两个公差带在左右任意飘的时候，两公差带相互之间的距离不需要保持72的距离，即两公差带相互之间的距离可远可近。

也就是说，图26的标注，设计者不想控制孔的左右位置，也不想控制两孔之间的中心距。所以可能会出现图27中的情况。

有小伙伴可能又要问了，假如功能需要，要求控制两孔之间的相对位置，设计工程师该怎么标注呢？

容易，根据我们前面一章讲的内容，增加一个修饰符号CZ， 即增加内约束就可以了，见下图：

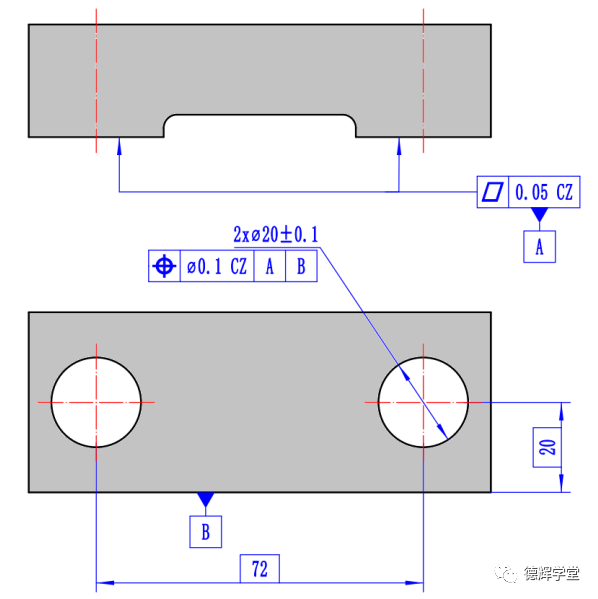
图28 既有内约束又有外约束

     见图28，因为增加了修饰符号CZ， 所以公差带在和基准保持理想的方位关系之前，首先需要相互之间必须保持理想的方位关系。即两个公差带尽管可以左右飘，但两公差带的中心距必须保持在72的前提下左右同时飘。见图29。

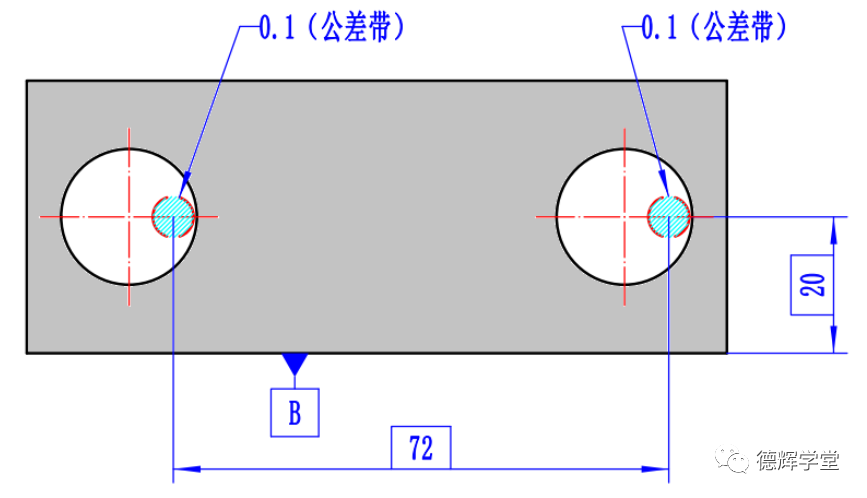
图29 既受内约束又受外约束的公差带

所以通过图26和图28的案例，我们会发现下面关系成立：

好了，我们通过这些案例的探讨，我们再捋一捋内约束和外约束的相互关系：

1. 内约束指的是公差带相互之间必须保持理想的方位关系，所以和外约束扯不上关系，内约束不可能具备外约束的能力。

2. 当来自基准的外约束能够约束公差带所有的非冗余自由度（Non-redundant freedom即有意义的自由度）的时候，外约束则能间接控制公差带相互之间的关系，具备内约束的功能。如本篇文章中的图24。

3. 当外约束不能约束公差带所有非冗余自由度的时候，外约束则不能控制公差带之间的相互关系。

我们再回到本公众号上期文章的主题，在什么前提下我们才能考虑增加内约束呢？显然，想要要求内约束，即增加修饰符号CZ/CZR/SIM，必须具备以下两个条件：

1. 被控制对象必须是两个或两个以上的特征组。

2. 公差带的非冗余自由度没有被外部的基准全部约束死或者根本就没有外部约束（没有基准）。

到目前为止，我们讲的都是内外约束的基本概念和各自的游戏规则，但是否应该采用内约束完全是由设计工程师自己决定，如何决定呢？我们接下来进入最后一节。

4. 内外约束应用的实际案例

     对研发工程师来说，必须根据产品的实际功能来决定是否需要增加内外约束的要求。比如图30中的行星齿轮系。

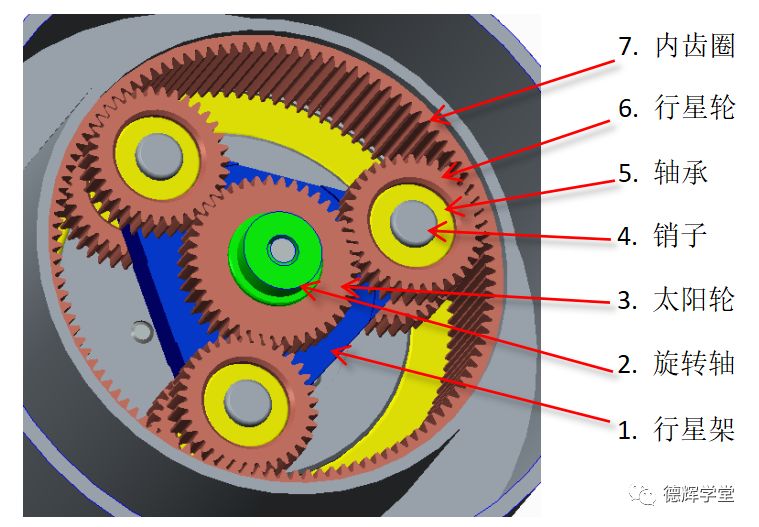
图30 行星轮系

根据对行星轮系的功能需求分析可知，行星轮与太阳轮，内齿圈的啮合非常重要。所以行星轮的位置非常关键，而行星轮是装在行星架上的，那么我们如何控制图31中行星架上的3个销子孔呢？

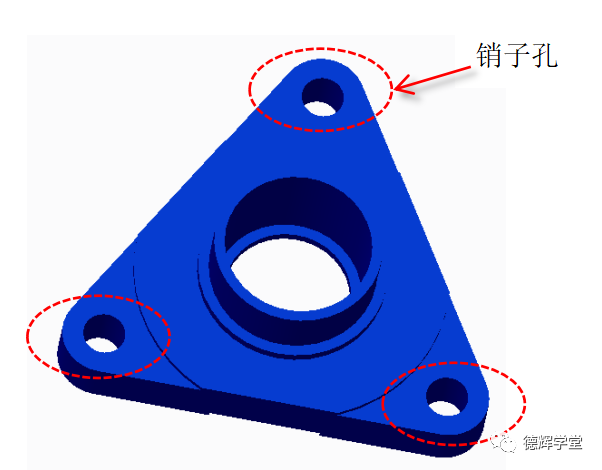
图31 行星架

行星架是通过中心孔和轴承装在轴上的，3个行星轮要顺利的拟合，除了需要和太阳轮保持相对的关系外，还需要相互之间保持关系（使得齿轮箱运动平稳和受力均匀）。

所以在控制行星架上的3个销子孔时，需要用外约束（以中心孔为基准）约束3个孔的整体位置，确保齿轮的正常啮合，还要用内约束控制3个孔相互之间的相对位置，确保行星轮分布均匀。

具体标注见图32。

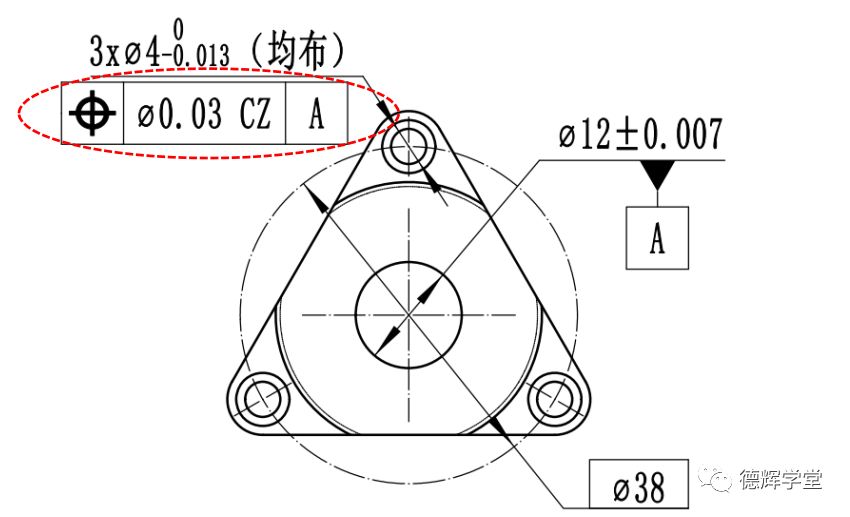
图32 行星架图纸

     图32中红圈部分的位置度标注，因为有内约束的修饰符号CZ, 所以首先要求3个直径为Φ0.03的圆柱型公差带相对关系要理想，即呈120度理想均匀分布在直径为Φ38的圆周上。然后三个相对位置固定的公差带作为一个整体，再和基准A保持理想方位关系，即和基准轴A（中心孔的最大内切圆柱轴线）绝对平行，且与基准轴A的中心距是19，这个约束关系就是来自于基准A的外约束。见图33。

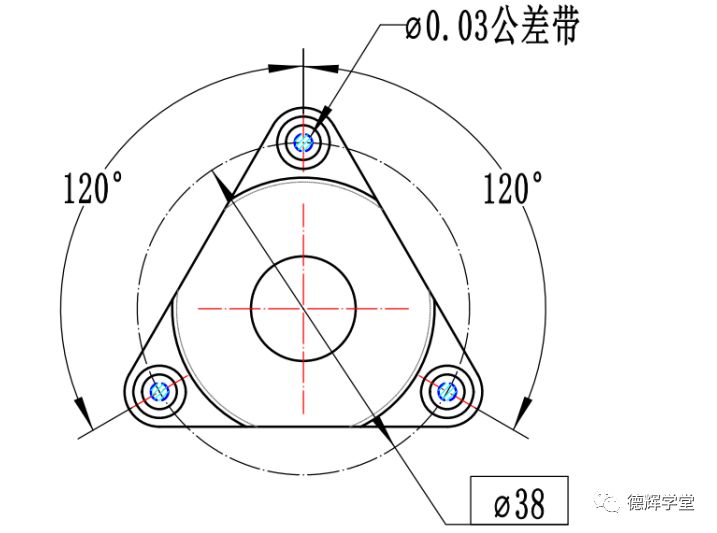
图33 公差带分布

图32的标注中，我们发现公差带还有一个旋转的自由度没有被约束，那就意味着公差带可以围绕基准A旋转。

     但是，因为有内约束CZ修饰符号的存在，如果旋转，要求3个均匀分布的公差带作为不可分割的整体必须一起旋转。见图34：

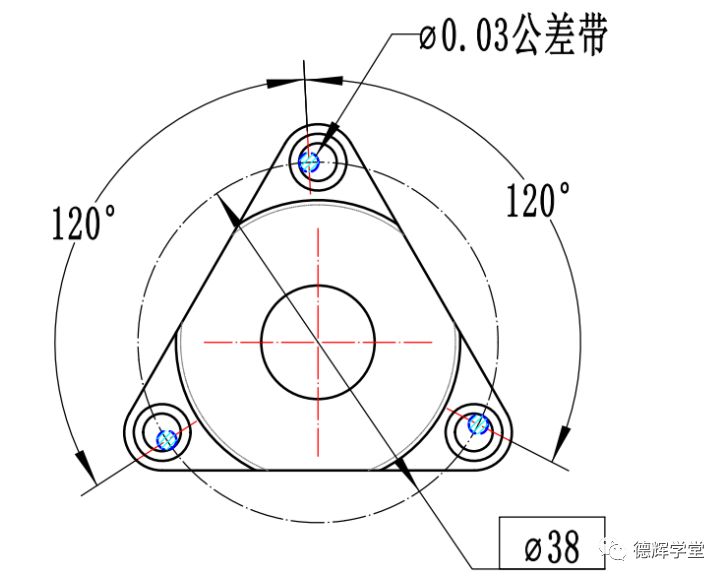
图34 一起旋转的公差带

所以，有了外约束，有了内约束，齿轮的顺利啮合和平稳运动就得到了保证。满足了功能的需求。

有小伙伴可能会问，不对啊，公差带如果任意旋转，意味着三个孔也一起旋转，那孔周围的壁厚是不是会变得太薄，影响强度呢？

确实有这种风险。

如果不正确控制，我们会发现，齿轮的啮合倒是没有问题了，但是零件的强度问题出来了。那怎么办呢？我们再把行星架的外轮廓给控制起来，并利用内约束管控外轮廓和3个孔之间的相对关系。

     也就是说，我们需要再增加一个内约束。这回我们采用SIM. 见图35。

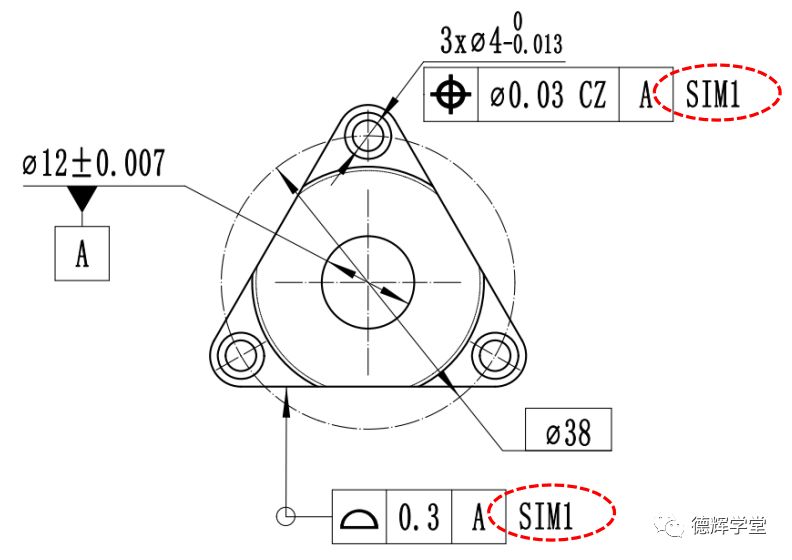
图35 采用同时要求的标注

图35中的标注，3个直径为Φ0.03的位置度公差带，因为CZ的原因，3个公差带相互之间受到内约束，同时所受到的内约束还有修饰符号SIM, 要求这3个圆柱形公差带不仅相互之间要保持理想的方位关系，他们仨和宽度为0.3轮廓度公差带也要保持理想的方位关系。除了内约束，位置度的公差带及轮廓度的公差带还受到来自基准A的外约束，需要和基准A保持方位关系。

也就是说，基准A约束了轮廓度公差带，也约束了位置度公差带，但是基准A自身的缺陷，导致轮廓度公差带或位置度公差带在围绕自身旋转方向上的自由度不能被约束。

即使加了SIM后，基准A同样不能约束公差带在旋转方向的自由度，但就是因为SIM的原因，位置度的3个公差带和轮廓度的公差带相互之间必须保持理想的方位关系，被牢牢“捆”在一起，可以围绕基准A一起旋转（注意，是一起哦）。见图36。

     这样，既解决了齿轮的啮合问题，平稳性问题，还解决了强度问题。

     其实，最终它们还是能围绕基准A旋转，该怎么办？那就随它去吧，旋转件不care。

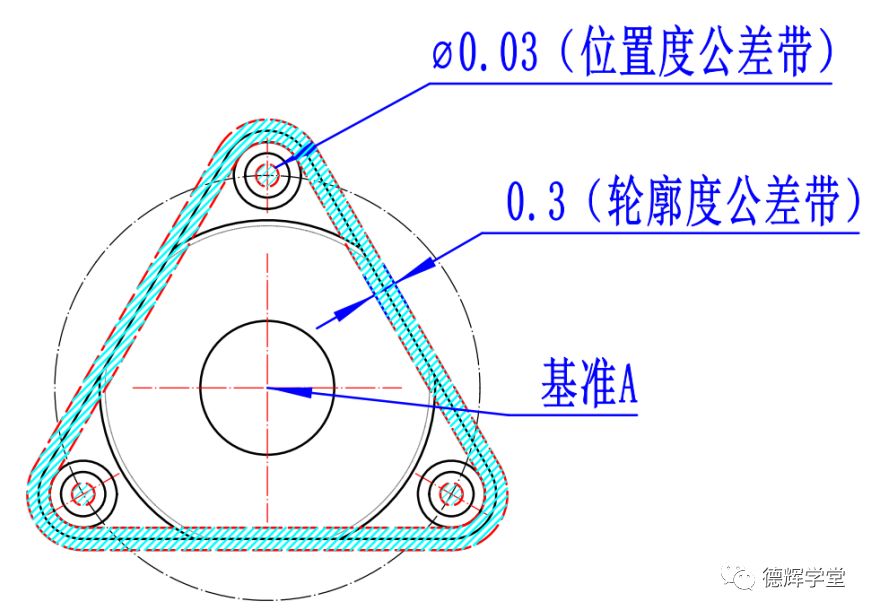
图36 采用同时要求的公差带

本章小结

本期文章是上期文章的继续。主要讲述了外约束以及内外约束的关系，首先所有来自基准的约束称为外约束，其次当几何公差在控制特征组的时候，如果来自基准的外约束能够约束公差带们所有的非冗余自由度的时候，外约束具备内约束的功能。否则，则不具备，因为外约束不能控制公差带相互之间的关系（这一点采用ISO标准的工程师们要特别注意，这是最新标准ISO 5458:2018颁布后的新规定，和以前不一样）。

     本期文章最后一部分以行星架作为案例，阐述了内约束和外约束同时采用的情形。