最小二乘直线，平面和圆是如何拟合出来的？

各位小伙伴，2025年新年好！好久没有更新公众号文章了。今天我们要讨论的话题是，最小二乘直线，平面，还有圆，是如何拟合出来的？

最小二乘法是高斯提出来，用处非常广泛，高斯大神曾经就用最小二乘法推算过谷神星的运动轨迹。

在GD&T的知识领域，ISO标准中,孔位置度的被测要素，就是每一层截面的最小二乘圆圆心的集合; 圆度的评价，除了采用切比雪夫法以外，也可以采用最小二乘法来评价（根据设计需求）。

今天的内容，我们就来仔细探讨一下这个最小二乘法。我们分三个部分来讨论：

1.     最小二乘直线的拟合

2.     最小二乘平面的拟合

3.     最小二乘圆的拟合

本期内容的数学味道比较重，对大家的数学基础，尤其是线性代数有一定要求，有兴趣的小伙伴需要耐心看完。

实在没有耐心，但工作中又要使用最小二乘法的小伙伴，也没有关系，可以直接跳过内容，在本文最后扫码，索要本文案例中提到的最小二乘法拟合的Excel表格，方便在工作中直接使用。

*****************

1. 1.     最小二乘直线的拟合

    *1.1理论部分*

    本期理论部分有点枯燥，但是会对最小二乘法的公式做严谨的推导。对数学实在有心理阴影的小伙伴，可以直接跳到第1.2部分，看实际操作。

本公众号往期的文章中，我们曾介绍过最小二乘法的公式（最后有链接）。本讲，我们以直线为案例，来看一下最小二乘法的基本逻辑和其公式的推导过程。

在一个平面上，假设我们知道4个离散点P1(x1, y1), P2(x2, y2), P3(x3, y3), P4(x4, y4), 我们想将它们拟合成一条直线，采用最小二乘法，该如何做呢？见图1：

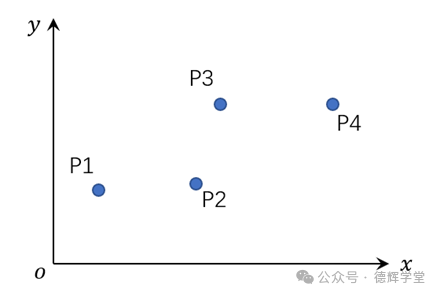
图1 4个离散的点

假设我们将4个离散的点已经拟合成一条最小二乘直线l1, 它的方程是y=kx+b, 其中k代表斜率，b代表截距，那么4个离散的点和这个直线l1之间，具备什么样的关系呢？

最小二乘法的特点，用数学的术语，叫“残差的平方和最小”。

我们还是说人话，见下图中的关系：

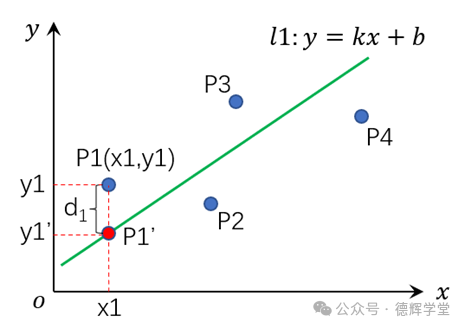
图2 最小二乘直线和残差

图2中，绿色的线l1就是最小二乘直线, P1（x1, y1）点中的是y1, 我们叫“观察值”（也就是测量值），我们将x1带入直线方程l1, 便得到新的点P1’ (x1’,y1’), 其中y1’，我们叫“估计值“。

图2中的绿色直线，是我们估计的直线，我们以为，所有的这些点，都“本来应该”分布在这条直线上，因为种种原因，实际上出现了偏差，这个偏差就是d1，这个d1也就是P1点对应的“残差”。

显然d1=y1-y1’, 又因为y1’=kx1+b, 所以有：

d1=y1-kx1-b      (1)

同样，p2, p3, p4,也对应有同样的残差d2, d3, d4, 见下图：

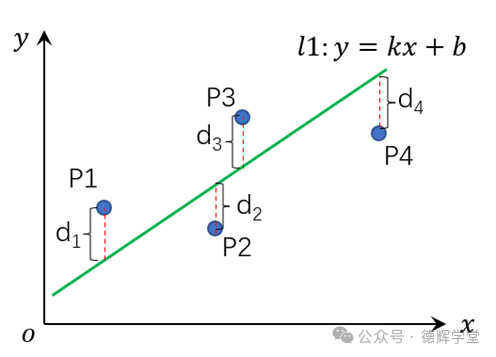
图3 4个残差

在图3中，我们假设：

J=d12+ d22+ d32+ d42 （这个就是残差的平方和）

如果图3中的绿色直线l1就是最小二乘直线，那么只有直线l1才能使得J的值是最小的！

注意哦，图3中的直线l1：y=kx+b, 其中k和b是未知的，它事实上有无数个可能性。如何找到合适的k和b，才能使得J最小呢？

这个时候，我们需要作数学处理。

所以，最小二乘法拟合的本质是：我们在寻找一个合适的直线，也就是寻求两个合适的参数：k和b，使得J最小。见动画1：

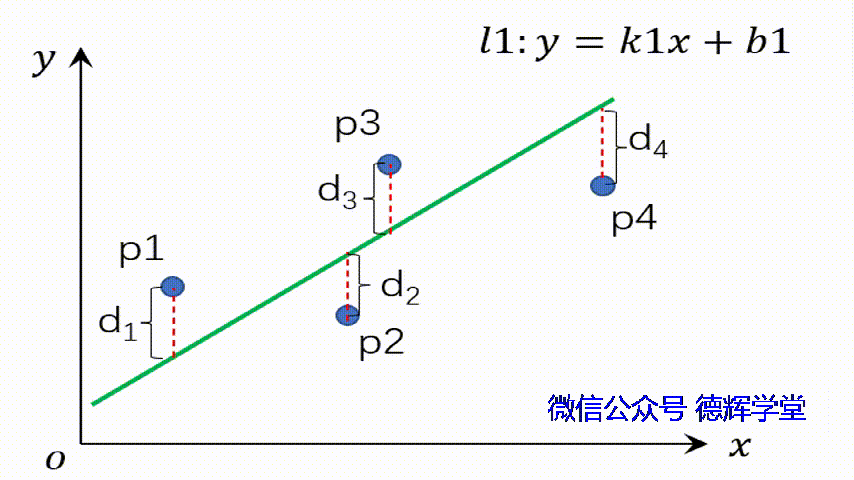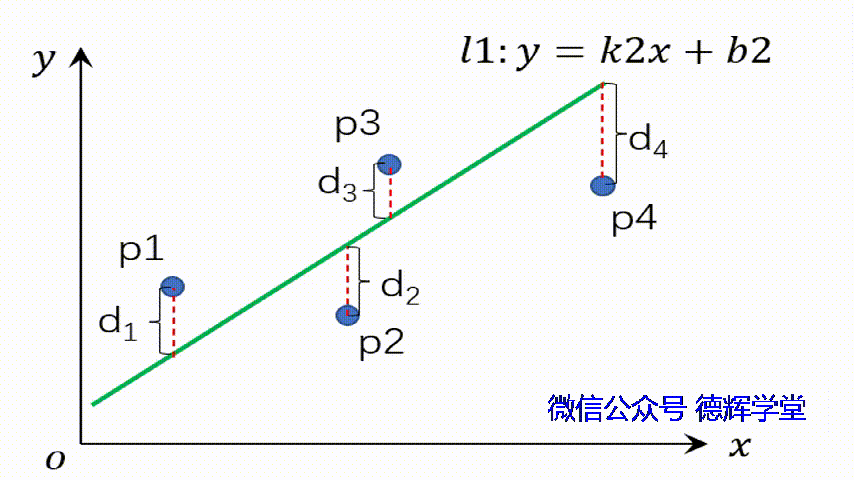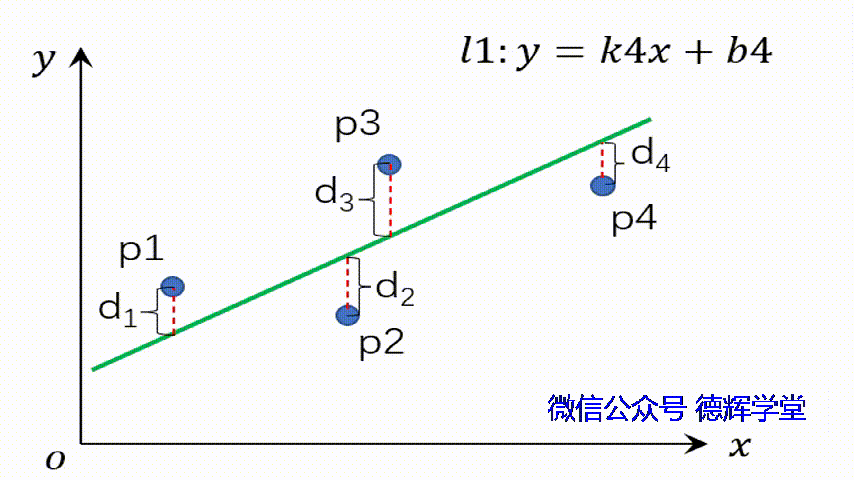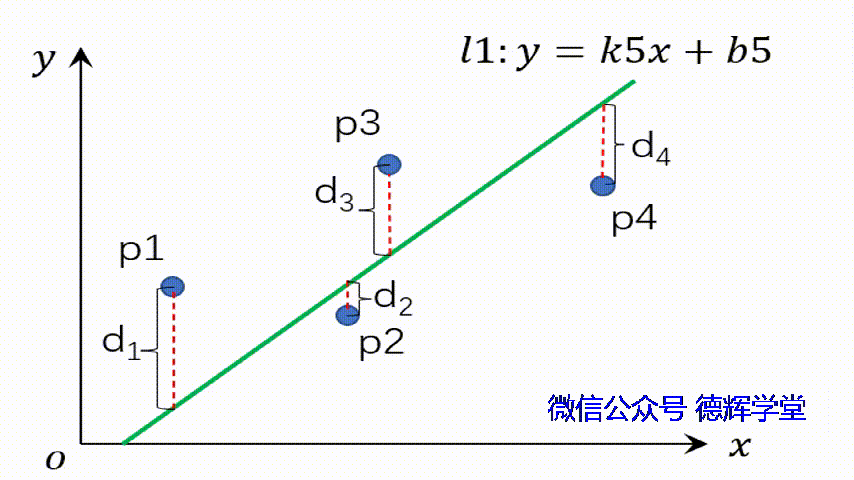
动画1 寻求一个合适的直线l1

注意，动画1中，k和b如果取不同的值，则直线的姿态和位置就会发生变化，对应的残差d1 d2, d3,d4也会发生变化，那么对应的残差平方和， 也就是J的值，也会发生变化哦。

而我们的目的，就是求得一个k, b值，使得J最小。

所以我们需要进行数学推导，推导如下：

根据公式（1）有：d1=y1-kx1-b

因为有4个测量点，就有4个残差，分别为：

d1=y1-kx1-b

d2=y2-kx2-b

d3=y3-kx3-b               (2)

d4=y4-kx4-b

接下来稍微做一个矩阵构建，设D=(d1,d2,d3,d4)T（右上标T表示转置）， D又叫残差向量，它是由4个残差组成的一个向量。

因为对于公式（2），我们想用矩阵来表达，所以先定义三个矩阵，X,Y,p:

令：

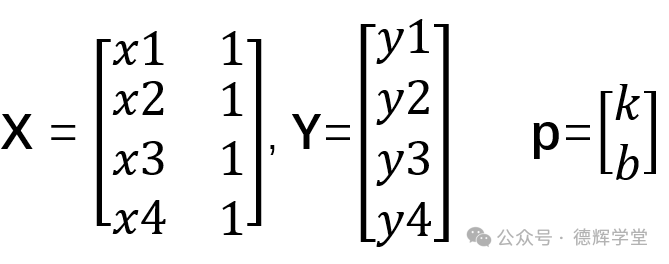
其中，p中的元素(k,b)就是我们要求的未知数。

把等式组（2）中的4个等式，可以用矩阵来表达：

D=Y-Xp             (3)

即：

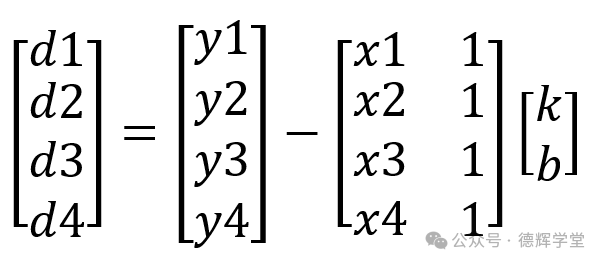      (4)

注意，上面的矩阵（4）和等式组（2）和是完全等价的。

因为我们的目的是使得残差的平方和最小，则需要先表达出残差的平方和来，所以有：

J=d12+ d22+ d32+ d42=DTD     (5)

注意，（5）式中 J是标量，它一个数值，D是一个nx1的矩阵，也就是残差向量，DTD相当于1xn的矩阵乘nx1的矩阵，结果是1x1的矩阵，也就是一个数值。

这就是转置矩阵的妙用之一。再表达一下：

J= DTD

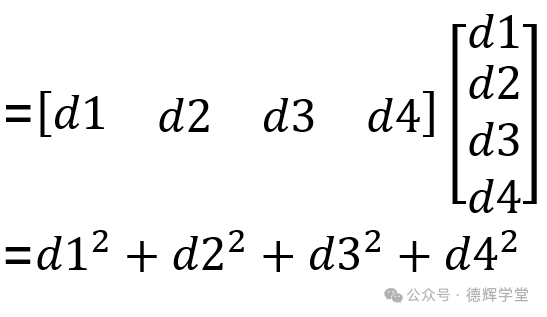
把式（3）中的等式D=Y-Xp，带入等式（5）， 则有：

J=DTD =（Y-Xp）T(Y-Xp)     (6)

公式（6）中，Y是已知的观察值（由离散点的y坐标构成），X也是已知的观察值（由离散点的x坐标和1构成），p是需要求的，所以（6）式可以写成函数的表达式：

J（p）=（Y-Xp）T(Y-Xp)     (7)

式（7）中，J（p）实际上是关于向量p的函数，又叫代价函数。注意，p是一个向量，它包含两个元素k和b.

p=

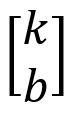
现在的我们的任务是，求得p值，使得式（7）中的J（p）最小。

尽管J（p）是关于p的向量函数，但是它的很多性质与我们普通函数类似，即自变量和因变量的性质一样。

比如，要求J（p）的极值，需要对p求导数。

先把公式（7）括号打开：

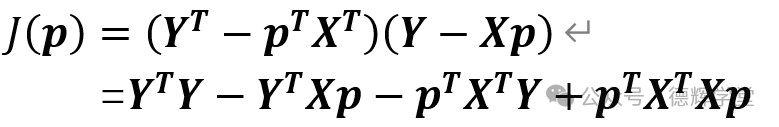 (8)

在上面打开的过程中会遇到关于转置的公式，比如(A-B)T=AT -BT ,  (AB)T=BTAT这样的基本定理，大家在研究的时候要注意。

公式（8）中，YTXp和pTXTY都是1x1矩阵，而且互为转置，所以两者相等，整理（8）得：

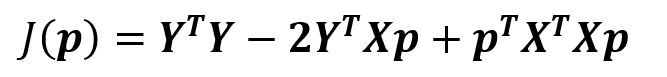（9）

在公式（9）中，对向量p求导（求极值都得求导）：

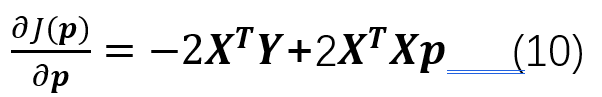
注意，式（10）中，对向量求导的结果，又要用到矩阵论里边的一些知识点:

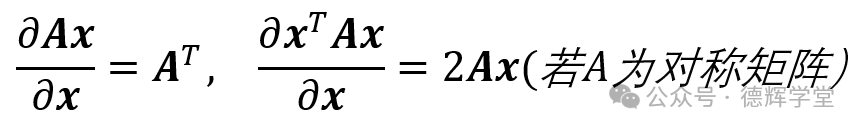
公式（10）中，因为偏导为零，才是J（p）的极值点（或驻点），所以令:

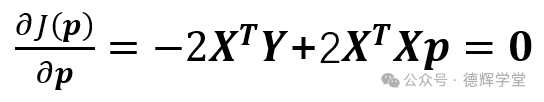
进一步得出：

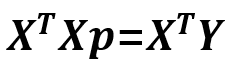
等式两边左乘(XTX)-1, 可以得出：

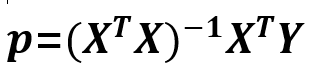     (11)

公式（11）就是最小二乘法的数学公式的推导结果，这是一个经典的公式，希望大家记住。

当然，严谨起见，还需要对公式（10）再对p求导，即对J(p)求二阶导：

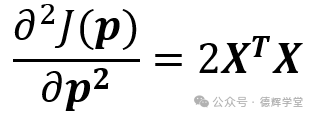
即海森（Hessian）矩阵H=2XTX, 因为X列肯定满秩（不可能4个点的x坐标都相同）， 所以海森矩阵H肯定正定。

讲到这里，可能有的小伙伴有点头晕，这里类似我们要知道一个函数的极值，首先要求一阶导为0，这可能是一个极值点，但是我们怎么知道它是极大值点，极小值点，还是只是一个驻点? 

所以通常还要求二阶导，二阶导如果大于0，那么一阶导为0的这个点，肯定是函数的最小值。

而在向量函数里边，海森矩阵正定，相当于二阶导大于0， 所以公式（11），也意味着当一阶导等于0时，推算出来的p值, 对应的是代价函数J(p)的最小值。

而代价函数J(p)表达的正是残差的平方和:

J=d12+ d22+ d32+ d42=DTD

所以公式（11）中的p值, 所对应的就是残差的平方和最小哦。我再把前边的图片放到下边：

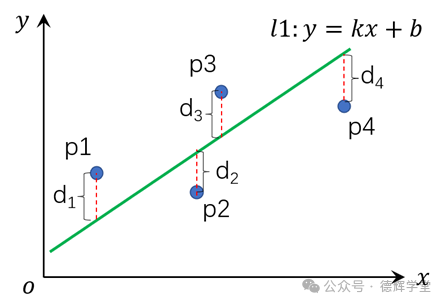
图4 4个残差d1,d2,d3,d4

利用公式（11）, 计算出p, 又因为p=(k,b)T, 就是说p包含两个元素k和b。那就意味着，我们求出p, 我们就是知道了k, b， 图4中的绿色的直线就确定了哦。我再把公式（11）写在这里：

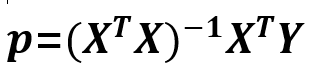 （11）

图4中，那条绿色的直线，就是我们心心念念的最小二乘直线！因为只有这条直线，才满足图4中的残差的平方和（d12+ d22+ d32+ d42）最小。

1. *1.2  实际操作*

2. 
   

好了，最小二乘法的理论讲完，我们再来讲实际操作。我们用最大众的软件，Excel来操作计算最小二乘直线，也就是要利用好公式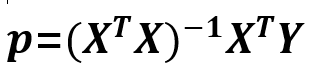（11）：

（11）

要利用公式（11）计算最小二乘直线，关键是，利用已知的点，只要能构建出正确的矩阵X和Y，再利用上面的公式（11），就可以直接算出p值。

比如已知离散的点如下：

P1(x1,y1)

P2(x2,y2)

P3(x3,y3)

P1(x4,y4)

根据前边的推导变换，则有：

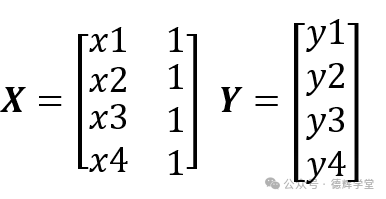
然后所谓矩阵的乘法，转置和求逆，我们直接利用EXCEL中现存的函数来完成就行。

比如，已知4个点的数据如下（实际上，可以有无数个点）：

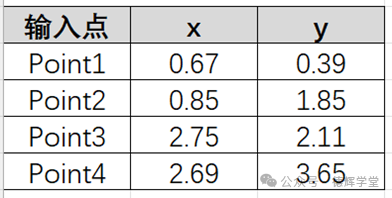
图5 原始数据

再利用Excel的特点，整理成两个矩阵X和Y，见图6：

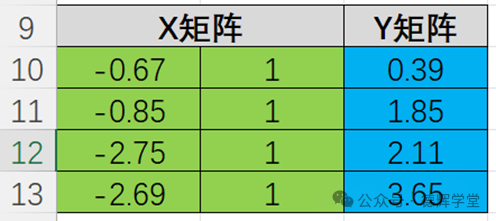
图6 X矩阵和Y矩阵

然后就可以计算了，在图7中的红框处，利用公式（11）计算p，可以用下面的EXCEL函数完成：

MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A10:B13),A10:B13)),TRANSPOSE(A10:B13)),C10:C13)

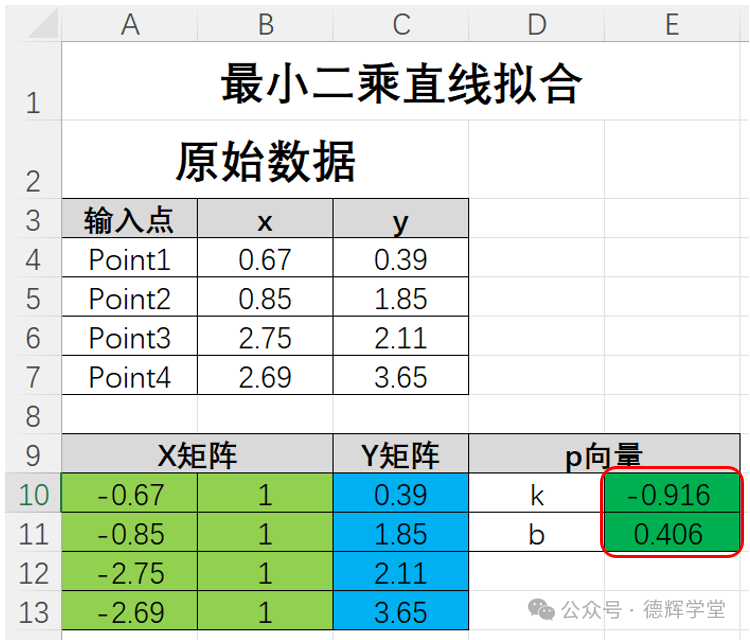
图7 计算最小二乘直线

先解释一下上面一长串Excel关于矩阵运算的函数：

MMULT(A,B)=AB

TRANSPOSE(A)=AT

MINVERSE(A)=A-1

那一长串函数，无非就是函数再套函数呗。

我们继续，图7中的k和b, 就是最小二乘直线的两个参数。拟合出来的直线如下图所示：

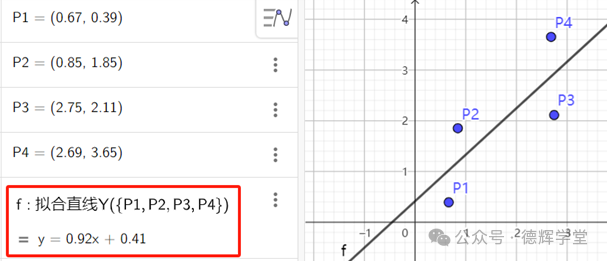
图8 拟合出来的直线

然后，我们就可以用它来近似计算直线度，或其他用途。

在最后，稍微总结一下: 我们只要把直线方程用矩阵相乘的形式来表达，就可以轻易构建出图6中的X矩阵和Y矩阵。

比如直线方程：kx+b=y，转化成矩阵的形式，则为：

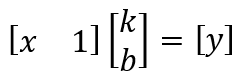
对应的矩阵代号为：

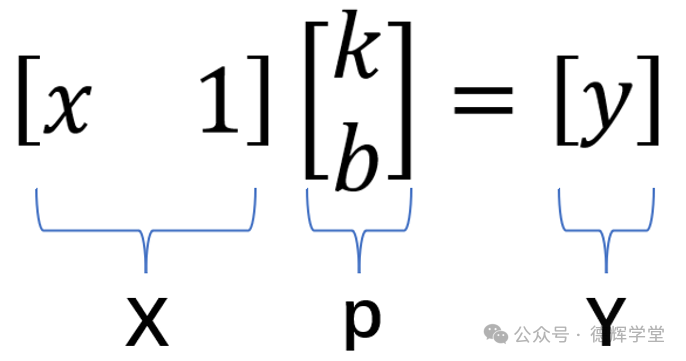
图9 直线方程对应的矩阵

如果p是由未知参数构成，X和Y是由已知的测量数据构成，则它们形成等式：

Y=Xp

那么就可以得出p的的最小二乘解：

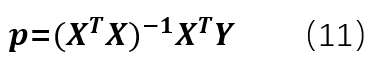
当然，前提是XTX可逆，这个我个人觉得不用担心，只要我们的测量点不重叠，肯定可逆。

根据我目前有限的经验，只要目标函数能够写成Y=Xp的矩阵形式，都可以直接套用公式（11），来计算p的最小二乘解。

平面方程也可以做类似的转换，然后构造矩阵X,p,Y, 弄成Y=Xp的形式，就可以利用公式（11）求解了。

接下来我们就来讨论最小二乘平面。

1. 2.     最小二乘平面的拟合

2. 
   

3. *2.1理论部分*

4. 
   

平面方程是：Ax+By+Cz+D=0

我们做一个转换，将平面方程两边除以C（C≠0）：

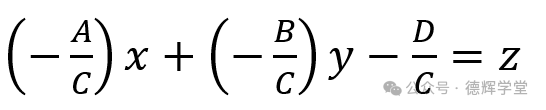   (12)

再令:

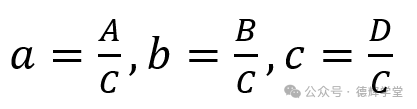     (13)

将（13）带入（12）则有：

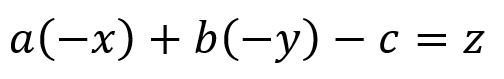
转化成矩阵格式：

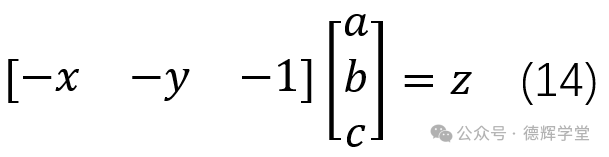
通过（14）， 我们可以构建出平面方程的矩阵形式：

Xp=Y

其中X=[-x -y -1]，p=[a b c]T， Y=z

和最小二乘直线的原理是一样的，而且也是用公式（11）来计算：

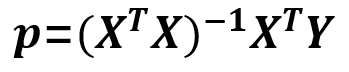   （11）

这里就不再做啰嗦的推导，有兴趣的小伙伴可以根据前面的套路自己再推导一遍。

*2.2实操部分*

同样，在实际操作时，如何用三坐标测量出来的离散的点P(x,y,z)来构建对应的矩阵X，矩阵p和矩阵Y非常重要.

假设有5个离散的点，他们的坐标是：

P1（x1,y1,z1）

P2（x2,y2,z2）

P3（x3,y3,z3）

P4（x4,y4,z4）

P5（x5,y5,z5）

根据上面转化的公式（14），则可以构建矩阵：

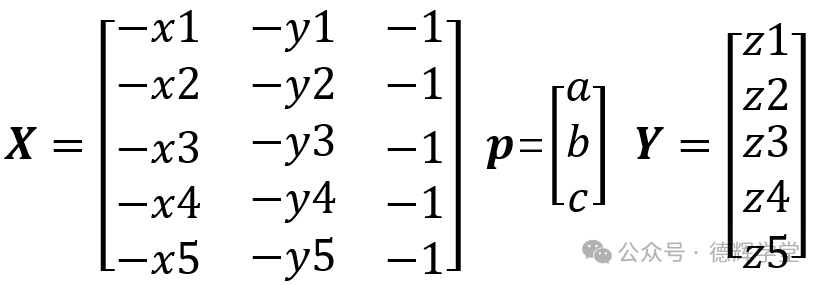
还是用Excel举例子吧：

下面5个点是三坐标在零件表面上采的5个点：

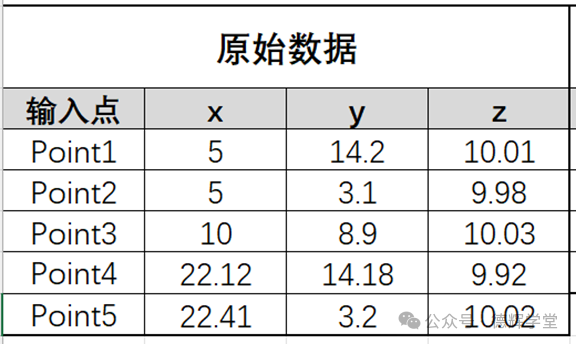
图10 三坐标采集的原始数据

利用Excel的特点，整理成X矩阵和Y矩阵：

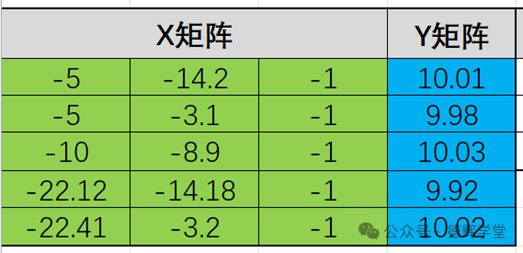
图11 整理成X矩阵和Y矩阵

X,Y矩阵有了，还是利用公式（11），在图11的红框处，输入一长串公式:

=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A11:C15),A11:C15)),TRANSPOSE(A11:C15)),D11:D15)

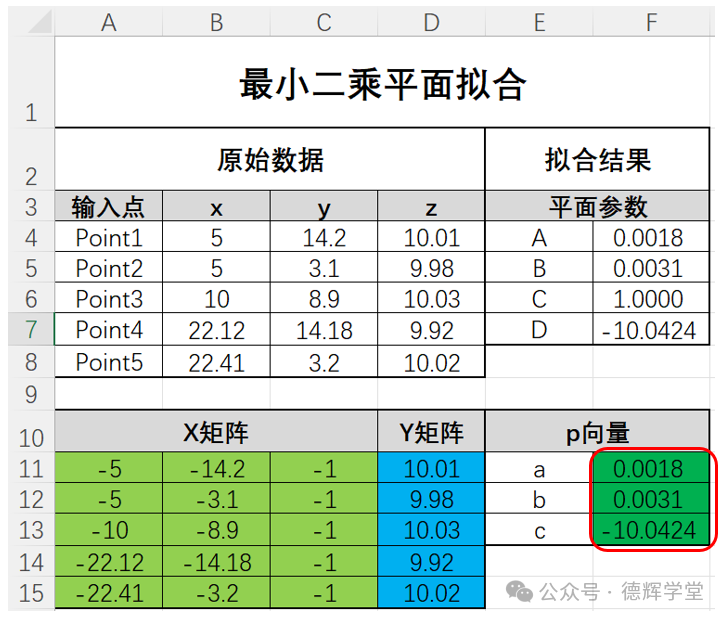
图12 计算参数a,b,c

对一个具体的空间平面，它的方程是：Ax+By+Cz+D=0，因为A,B,C,D可以等比例的放大或者缩小，它不影响平面的性质，所以A,B,C,D的值不是唯一的。

为了方便计算，设C=1， 然后利用已经计算出来的 a=A/C, b=B/C, c=D/C, 从而再计算出平面参数A,B,C,D的大小, 见图11中A，B，C，D的数值。

这个最小二乘平面拟合出来干什么呢？可以根据设计的图纸需求来，比如做基准面（近似测量），比如作为平面度的近似理想要素, 等等。

1. 3.     最小二乘圆的拟合

2. 
   

接下来就要讨论我们的重点，最小二乘圆的拟合。

*3.1 理论部分*

和最小二乘直线的原理一样，假设我们有一堆散点，P1, P2, P3, P4, P5, P6 我们想把这些点拟合成一个最小二乘圆，应该如何做呢？

先来理一下逻辑，所谓最小二乘圆，就是一个特殊的“平均圆”。

动画2 最小二乘圆

这个“平均圆”它有个特点，那就是P1-P6到这个圆的距离的平方和（又叫残差的平方和）最小。

见下图：

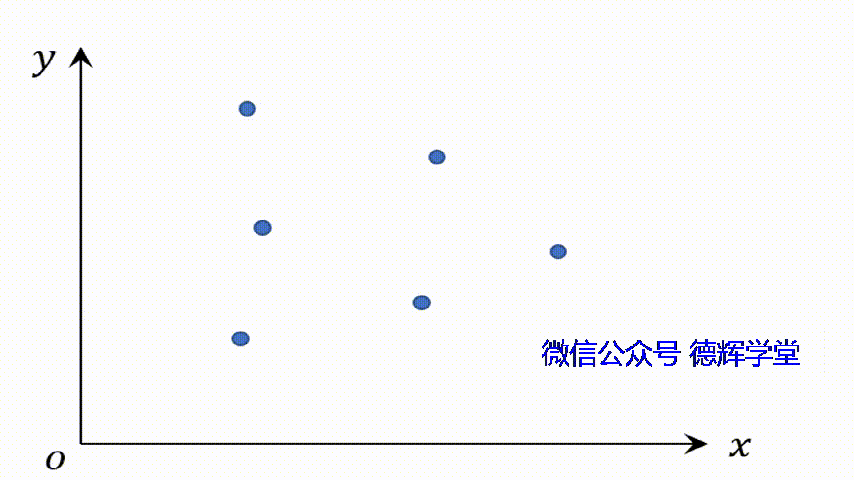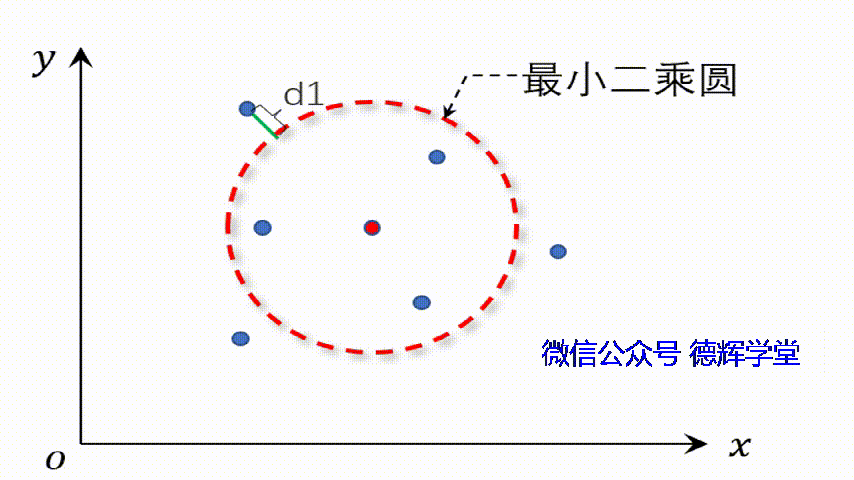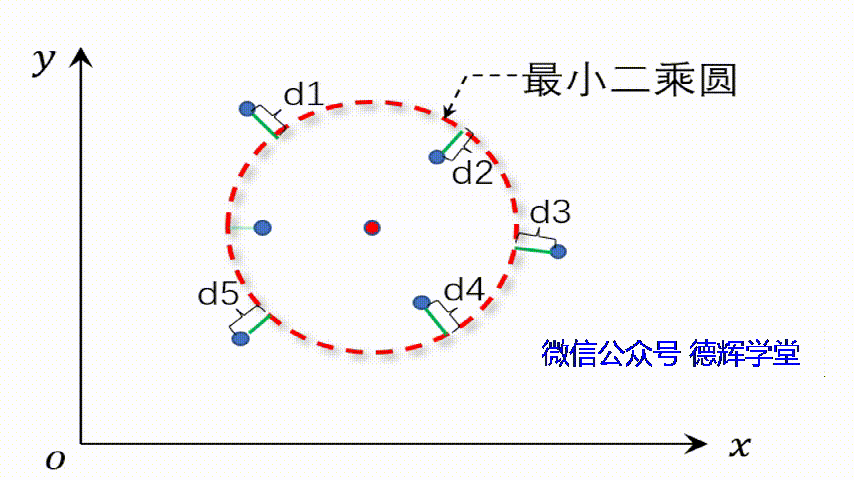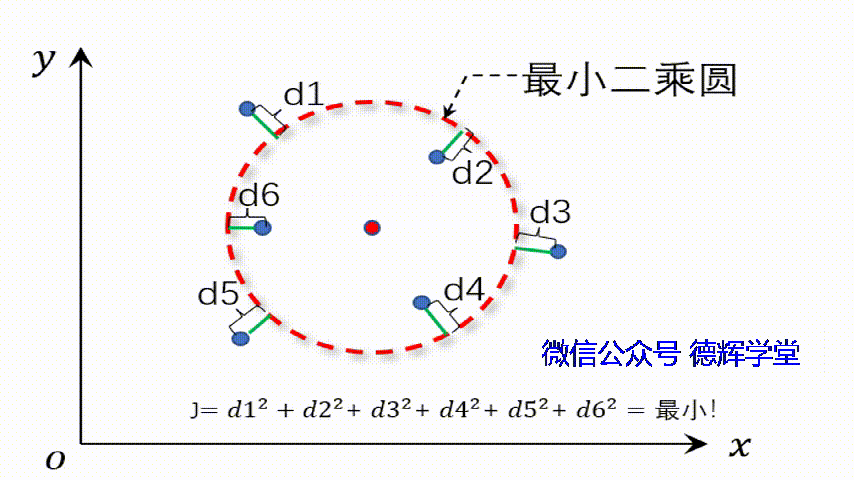
动画3 最小二乘圆的特点

因为平面圆的方程是(x-A)2+(y-B)2=R2,其中A,B为圆心坐标，R为半径。所以寻求最小二乘圆的过程，实际上就在寻找不同的圆（对应的就是不同的参数：A,B,R）, 最终使得残差的平方和最小。

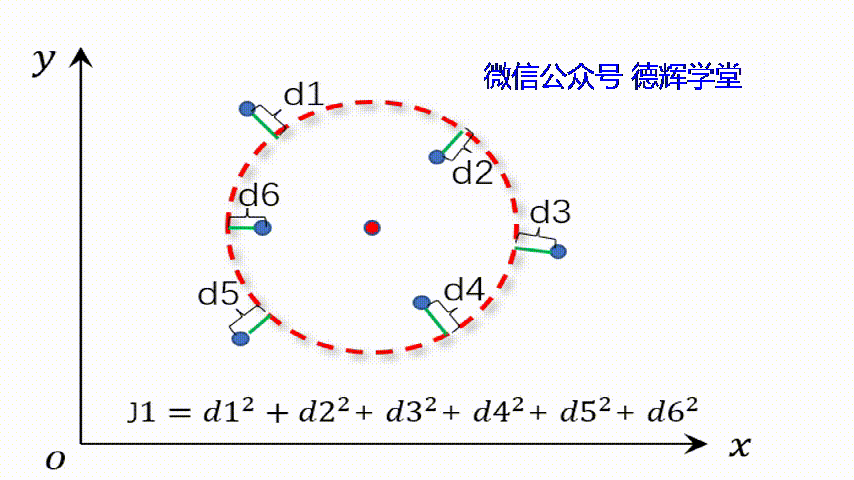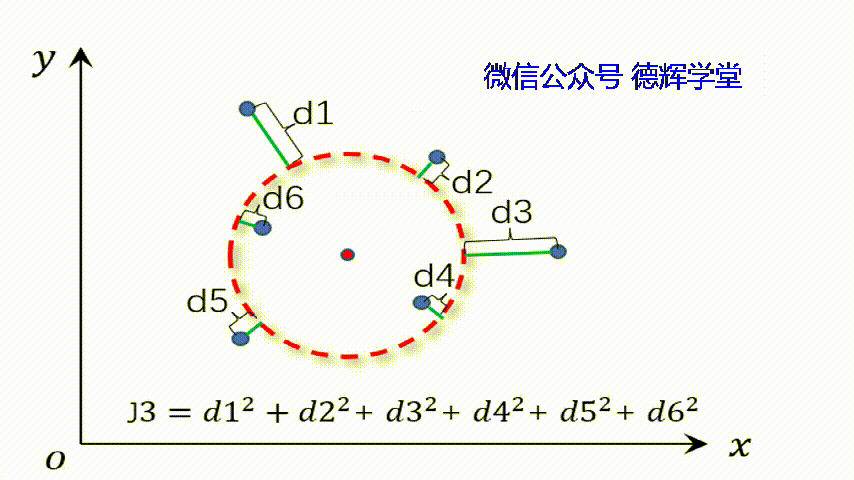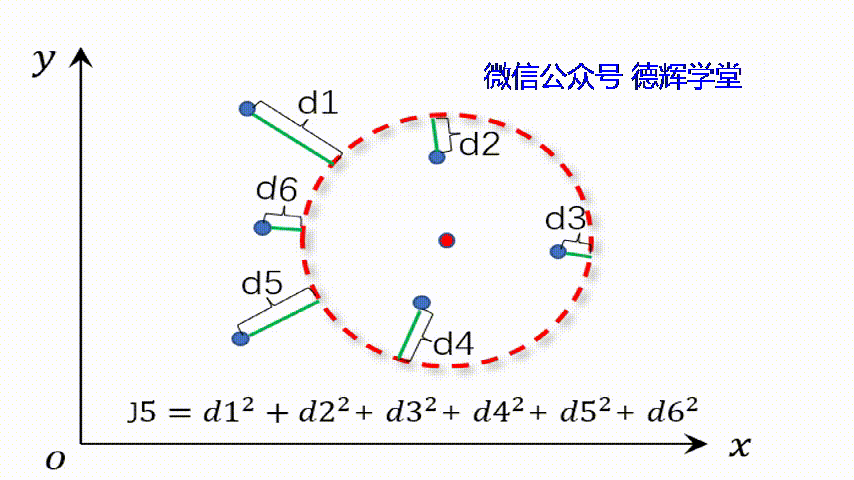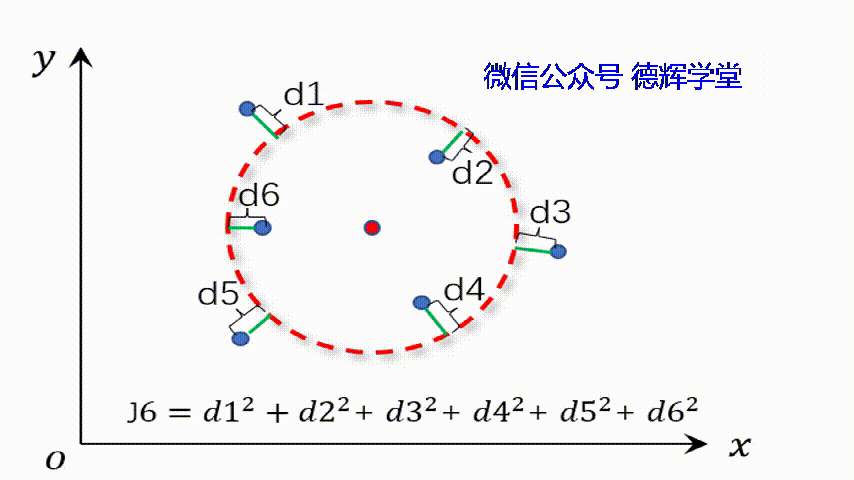
动画4 寻找最小二乘圆

我们先假设最小二乘圆的方程就是(x-A)2+(y-B)2=R2，先求出残差，也就是每个离散的点到这个圆的距离，理论上应该是离散点P到圆心O(A,B)的距离, 然后再减去R。

以P1(x1, y1)作为案例，相当于d1=P1O-R, 见图13.

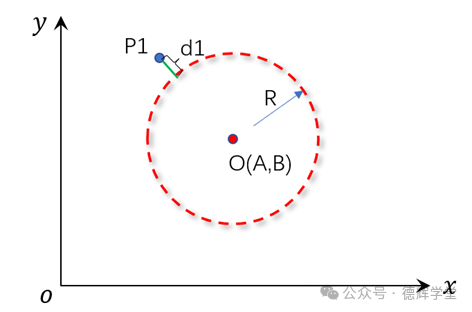
图13 计算残差d1

因为计算距离P1O要开根号，处理起来非常麻烦，我们做一个妥协，用距离的平方来代替距离，半径的平方来代替半径，平方差d1’来代替残差（貌似数学界都这么近似处理，不影响性质）：

d1’=P1O2-R2

那么d1’=(x1-A)2+(y1-B)2-R2

接下来就是和前面一样枯燥的推导过程，不耐烦的小伙伴可以跳过这一段，看后边的实操部分：

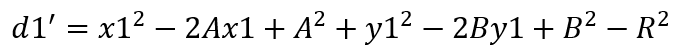
整理得：

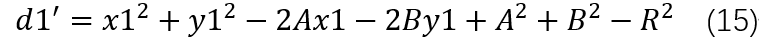
重组一下参数：令a=-2A, b=-2B, c=A2+B2-R2

则公式（15）可以简化成：

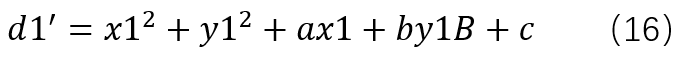
上面的等式是不是有点熟悉？因为可以写成矩阵的形式：

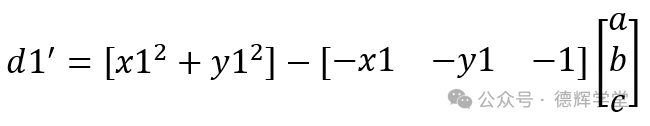
现在呢，有6个点（P1-P6）, 有6个残差，利用公式（16），先弄个方程组出来吧：

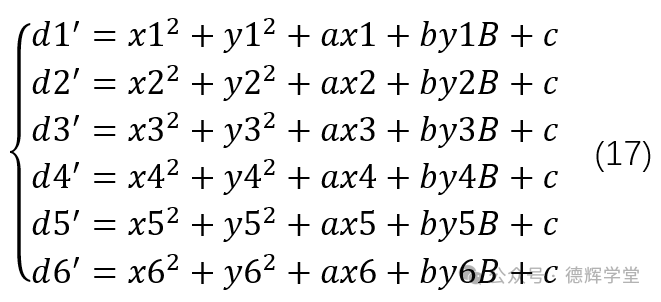
方程组（17）是一个超定方程组，或者说是一个矛盾方程组，肯定没有正儿八经的解，只有近似解。不管它，先转化成矩阵格式:

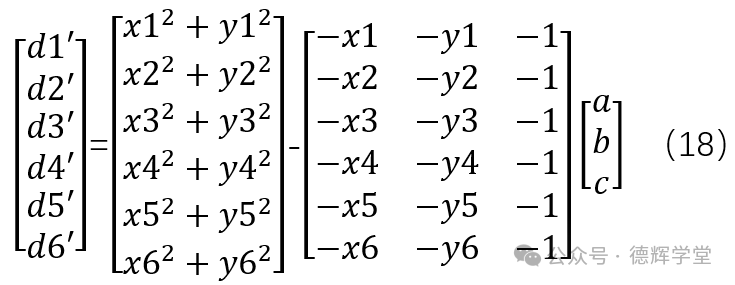
大家不要被上面的矩阵吓到，在Excel里边，处理起来就是输入数据，然后动动鼠标的事情。上面庞大的矩阵我们再做一个简化：

图14 矩阵简化

图14中，D就是残差向量，Y和X就是观察值构成的矩阵，也就是三坐标在零件圆周上采的点的坐标，它们所构成的矩阵。

p相当于一个自变量, 它包含了圆的三个参数, 圆心坐标A,B和半径R。注意p的元素，a, b, c, 就实际上包含这三个圆的参数, 无非就是做了一个转化。

所以，基于图14，公式（17）可以写成下面的简化形式:

D=Y-Xp

还是按照老套路，先构建代价函数J(p):

J(p)=d12+d22+d32+d42+d52+d62= DTD

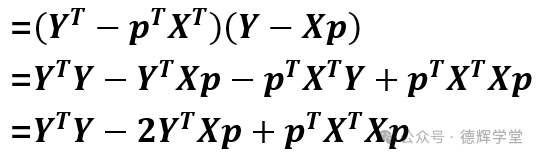
同第一讲一样，然后对p求偏导，并令偏导为0

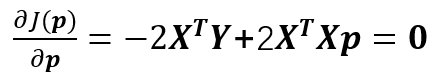  （19）

然后得出代价函数J(p)，也就是平方和处于极值时，所对应的p值：

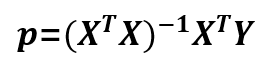  （20）

另外，前面已经证明过了，如果对公式（19）再对p求导，可以得出海森矩阵为2XTX, 在列满秩的前提下（现实中肯定列满秩）是正定的，所以上面的公式（20）对应的就是代价函数J(p)的最小值，证毕。

上面啰里八嗦的推导了半天，无非就是为了证明其严谨性。事实上，圆的方程（也就是目标函数），也可以整理成矩阵乘积的形式。

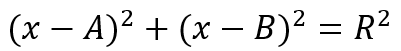
整理可得：

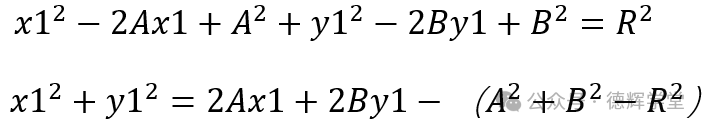
再做参数重组，令a=-2A, b=-2B, c=A2+B2-R2,则有:

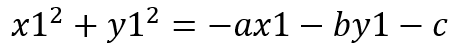    (21)

再令Y=x12+y12, X=(-x1 -y1 -1), p=(a,b,c)T

于是，公式（21）可以转化成下面格式：

Y=Xp

即圆的方程也可以用下面的矩阵相乘来表达：

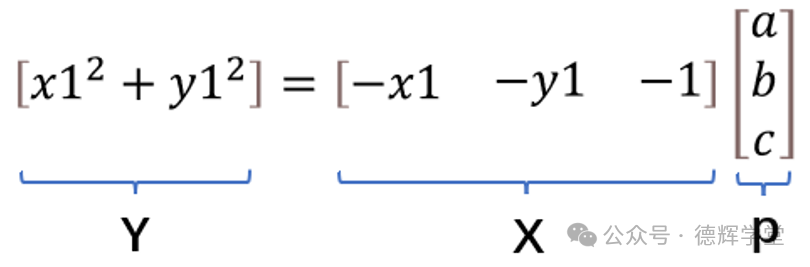
然后我们求p的最小二乘解，就可以套用下面经典公式：

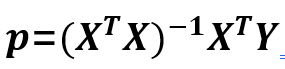    (20)

*3.2 实操部分*

同样的，我们用Excel来玩最小二乘圆。

关键点还是构建正确的矩阵X,Y和p，我把图14拷过来，见下图：

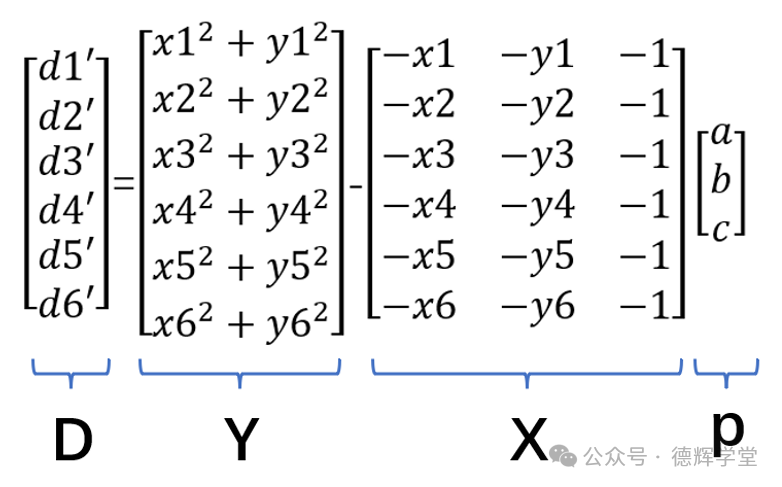
图14 矩阵转化

假设我们在一个零件孔的圆周上采了6个点，具体坐标如下：

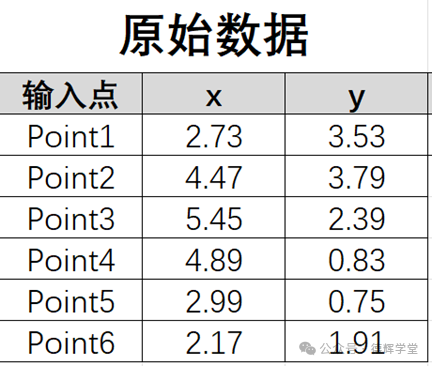
图15 原始数据

再利用Excel的特点，整理成X，Y矩阵：

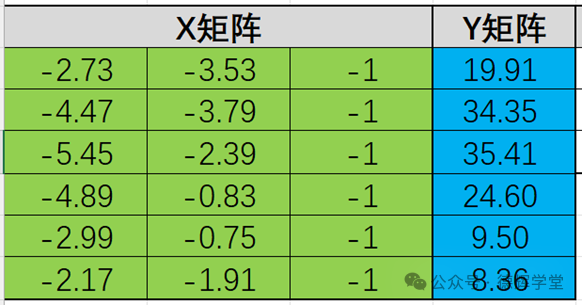
图16 整理成X矩阵和Y矩阵

同样的套路，在图17的红框处(也就是p的值)输入:

=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A12:C17),A12:C17)),TRANSPOSE(A12:C17)),D12:D17)

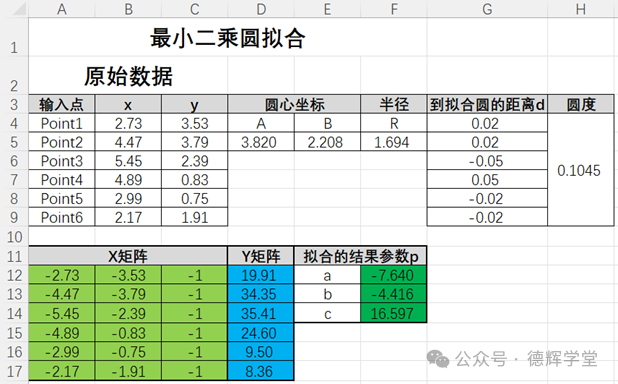
图17 拟合的结果

然后就得到了p的值，也就是知道了a,b,c的值，再利用参数重组时的公式：

a=-2A, b=-2B, c=A2+B2-R2

反推A,B,R,结果见图17，欧了。

最小二乘圆不仅仅在拟合提取中心要素（ISO标准）中会用到，也可以用来计算圆度（如果图纸要求用最小二乘圆来计算），见上图。

好了，今天的内容就到这里，能坚持看到这里的小伙伴，为您们点赞！

本期文章中的实操案例，已经做成Excel表格，欢迎各位小伙伴私我索要，或者扫描本期文章后边的二维码加好友索要哦。

内容回顾：

本期内容主要讲解了如何用最小二乘法拟合直线（平面直线）， 平面和圆。第一讲，我们讲解了最小二乘法拟合直线的逻辑，推演出了公式，最后用Excel表格拟合最小二乘直线；第二讲，我们讲解了用最小二乘法拟合平面以及实操；第三讲，我们讲解了如何用最小二乘法拟合圆，并再次推导了它的公式，以及如何用Excel实现。

***

在本文的最后，给您留一道思考题：我们前面讲的直线拟合，实际上仅仅局限于平面直线。如果给您空间中的离散点，您如何把他们拟合成一条空间的直线呢？欢迎您在留言区给我们留言。