您真的了解GD&T中的局部实际尺寸吗?
GPS(ISO标准)中,尺寸公差的两个极限尺寸的类型,默认为LP。此外,还允许在图纸上标注截面尺寸、局部要素尺寸、球面尺寸等,并对这些局部尺寸做了详细的规范,满足了对各种产品功能需求的表达。
那么在美标中该如何表达同样的局部尺寸呢?具体的规范是怎么定义的呢?
遗憾的是,在GD&T(ASME Y14.5)中,局部尺寸种类很少,且没有明确给出局部实际尺寸的定义与应用条件,给广大的设计工程师、测量工程师带来很大的困惑。
为此,依据ASME标准与个人理解对局部尺寸进行总结。欢迎各位读者来拍砖!
由于内容有点冗长,如果大家对标准解读不感兴趣,或对局部尺寸的产生不感兴趣,为节省时间,可以直接跳到第三节。
***1、局部实际尺寸的产生***
在ASME Y14.5.1-2019的2.3 Actual Local Size Limits中,局部尺寸分为两点尺寸(相对点对距离)和截面尺寸,并对其生成过程,进行了规范。
1.1 圆柱的两点尺寸生成
依据ASME Y14.5.1-2019的2.3.3.1 Establishing the Local Size Spine和2.3.3.2Evaluation of Actual Local Size (Opposed Points)对两点尺寸进行总结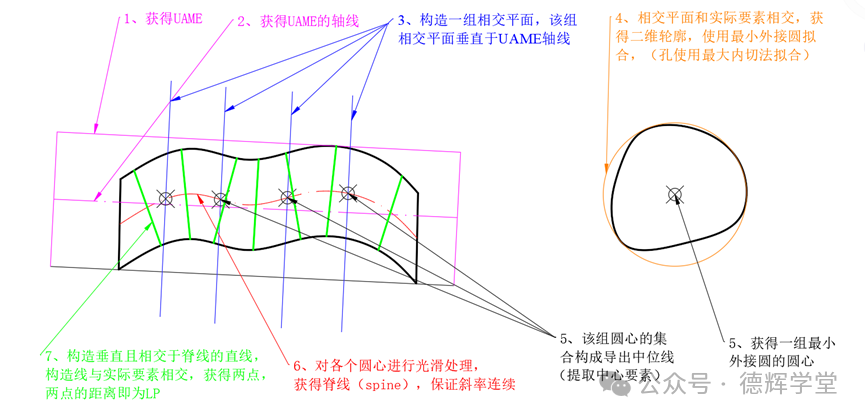
图1 两点尺寸的生成
如图1所示,以轴为例,描述生成步骤:
1)对实际要素进行最小外接拟合,获得对应的UAME。
2)获得UAME的轴线。
3)构造垂直于UAME的轴线的一组相交平面。
4)将上一步获得的相交平面集与实际要素相交,获得2D截面轮廓线(GPS术语:2D组成要素)。对于外要素,对2D截面轮廓线使用最小外接法进行拟合。
5)第4步获得的最小外接圆的圆心集合,构成GD&T中的导出中位线(类似GPS中的提取中心要素,美标中的直线度的被测要素就是此中位线)。
6)对第5步的圆心集合进行拟合,得到脊线(spine,不知道翻译的对不对),要求脊线的斜率要连续,保证LP尺寸能够覆盖过整个圆柱面。
7)构造相交且垂直于脊线的直线,构造直线与零件实际要素相交,得到2个交点,交点间的距离为LP。
值得注意的是:根据标准的描述,要求第7步先构造垂直于脊线的相交平面,然后在相交平面内构造直线,要求直线经过脊线。笔者认为这和上面的生成过程是一致的,经过且垂直于脊线的构造线,肯定位于垂直于脊线的平面内。
1.2 圆柱的截面尺寸的生成
截面圆的尺寸生成过程和两点尺寸生成过程差不多。如下图所示。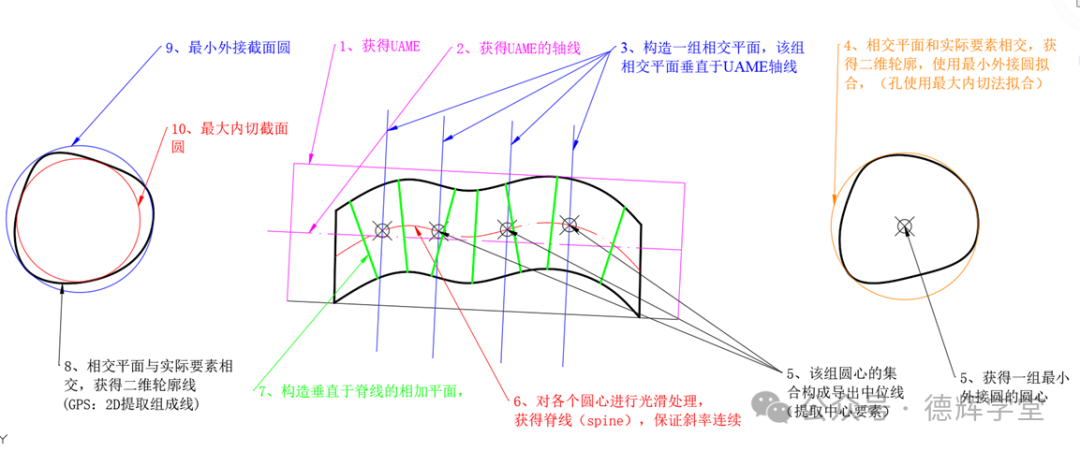
图2 截面圆的尺寸的生成过程
同样以轴为例,描述截面圆尺寸生成步骤,如图2所示:
1)~6)与两点尺寸的生成过程没有区别。
7)生成一组相交平面,相交平面与脊线垂直。
8)相交平面与实际要素相交,获得二维轮廓线(GPS术语:2D组成要素)
9)对各个二维轮廓线,采用最小外接法拟合,获得最小外接截面圆。
10)对各个二维轮廓线,采用最大内切法拟合,获得最大内切截面圆。
1.3 宽度的局部尺寸
ASME Y14.5.1-2019中,对宽度(两相对平行平面)也规定了两点尺寸,具体过程与图1类似:
1)对实际要素进行拟合(内要素:最大内切法;外要素:最小外接法),得到UAME(平行平面);
2)获得UAME的对称中心面;
3)构造一组直线,直线垂直于UAME的对称中心面。每条构造直线与实际要素相交,得到两个交点,计算两个交点的中点。
4)第3步获得了中点集合,构成了GD&T中的导出中位面(即GPS中的提取中心要素)。
5)对第4步的导出中位面进行拟合,得到脊面(spine),要求脊面的斜率要连续,保证LP尺寸能够覆盖过整个圆柱面。
6)构造垂直于脊面的直线,构造线与实际要素相交,得到2个交点,交点间的距离为LP。
ASME Y14.5.1-2019中,对宽度(两相对平行平面)没有规定截面尺寸(两平行线的距离),如图4所示的标准描述。这是因为如果获取2D组成要素,需要构造相交平面,相交平面需要垂直于脊面,但脊面是个曲面,无法构造相交平面。GPS则不同,2D提取组成要素的相交平面是垂直于拟合中心要素(理想平面)的,因此在GPS中,宽度的截面尺寸是存在的。
***2、ASME的局部尺寸与ISO的局部尺寸的差异***
由于本文主要介绍GD&T中的局部实际尺寸,由于篇幅所限,本文只给出圆柱的局部尺寸的生成过程。主要参考以下文献:《(产品几何技术规范(GPS)通用概念第3部分:被测要素GB/T24637.3—2020)》。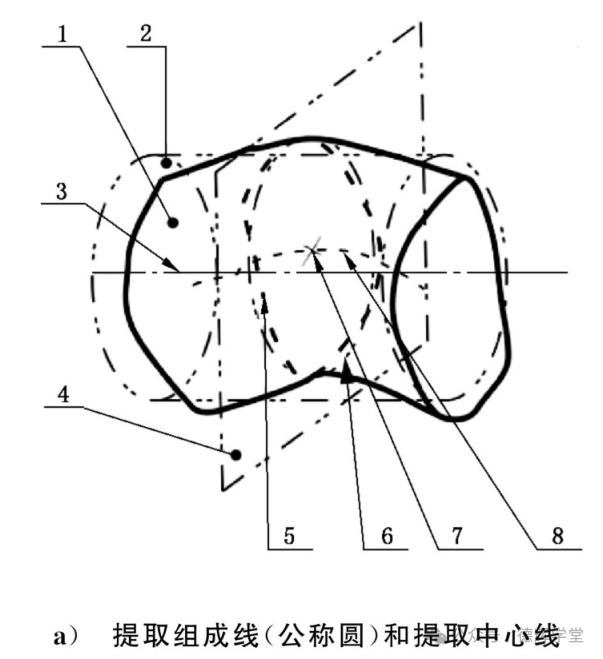
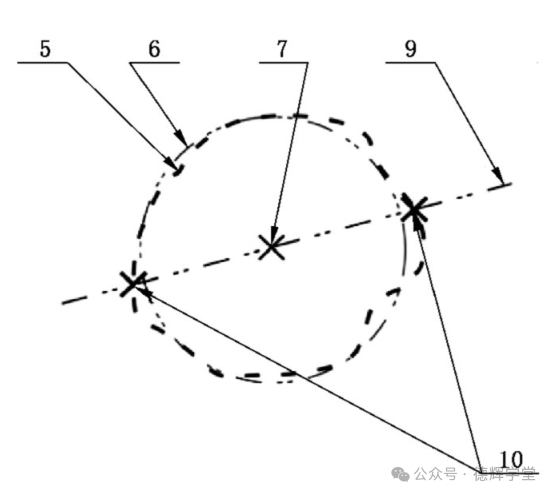 图3 GPS中两点尺寸与截面尺寸的生成
图3 GPS中两点尺寸与截面尺寸的生成1)在实际要素上采点,获得提取组成面1。
2)默认采用最小二乘法,对提取组成面1进行拟合,得到圆柱面2。同时,获得其轴线3(拟合中心要素)。
3)构造一组相交平面4(标准中称其为主使能要素),相交平面垂直于轴线3。
4)相交平面4和要素相交,获得二维轮廓线,称为提取组成线5。
5)对提取组成线5拟合(默认是最小二乘法),获得拟合圆6。同时,获得拟合圆的圆心7。拟合圆6的尺寸即为圆柱的截面尺寸,可以使用最小外接法、最大内切法、最小区域法、最小二乘法等拟合,可以通过尺寸公差标注进行规范。
6)圆心7的集合构成提取中心线8。
7)在相交平面内,构造直线9(标准中称其为辅助使能要素),要求直线9通过拟合圆心7。
8)直线9与实际要素相交,得到两个交点10,这两个交点的距离就是LP。
由此可以总结出ASME和GPS对局部实际尺寸的定义的不同,见表1。
表1 GD&T和GPS中局部尺寸的不同点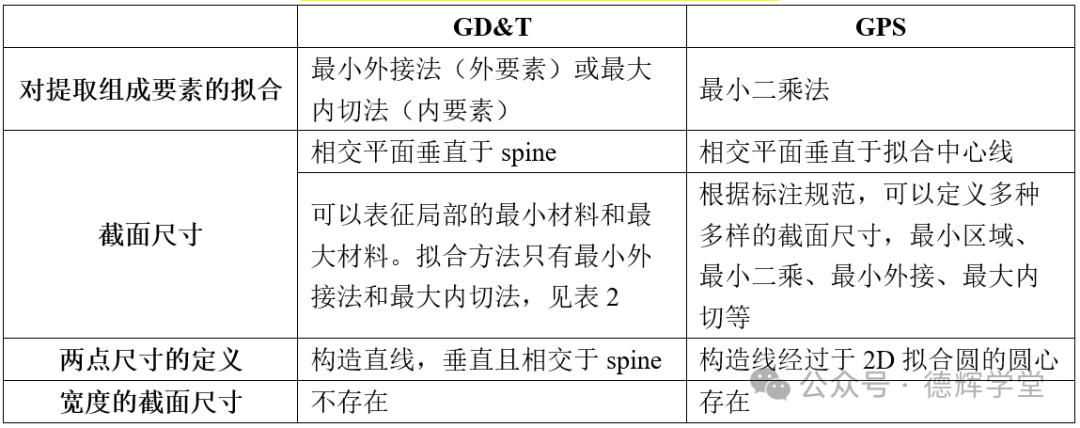 ***3、局部实际尺寸的应用***
***3、局部实际尺寸的应用***前面都是令人费解的理论,大家了解即可。对产品设计工程师或测量工程师来讲,最关心的是:到底什么场合下使用两点尺寸作为局部实际尺寸那,什么场合下使用截面尺寸作为局部实际尺寸那?截面又分为最大内切尺寸和最小外接尺寸,到底使用哪一个?
本文将从规则尺寸要素和不规则尺寸要素两方面讨论,讨论的切入点是要素自身的几何特性以及算法的适用条件,没有讨论具体的产品功能。
3.1 规则尺寸要素的极限尺寸类型
表2 规则尺寸要素的极限尺寸类型
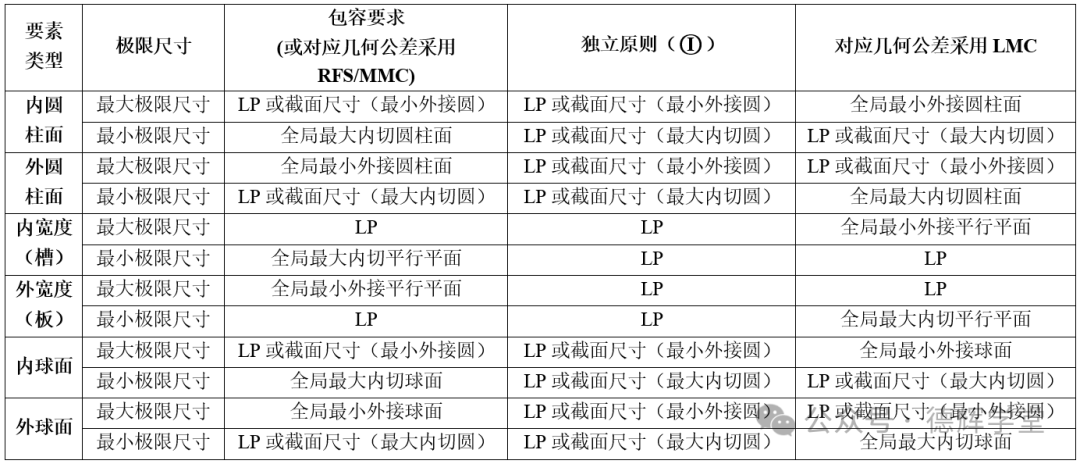
以内圆柱面为例,介绍其尺寸公差中极限尺寸的尺寸类型,如表2所示:
1)对于应用了包容原则的内圆柱面,最小极限尺寸对应的尺寸类型为全局最大内切圆柱面的尺寸,而最大极限尺寸对应的尺寸类型为局部实际尺寸,具体是两点尺寸还是截面尺寸?遗憾的是,ASME标准中,并未明确规定。但是,标准中说明了,如果采用截面尺寸作为局部实际尺寸,则最大极限尺寸采用最小外接截面圆的尺寸(最小材料对应的局部实际尺寸)。如图4所示。
2)对于应用了独立原则的内圆柱面,两个极限尺寸均为局部实际尺寸,可以是两点尺寸或截面尺寸。同样,如果局部实际尺寸采用截面尺寸,最小极限尺寸采用最大内切截面圆的尺寸,最大极限尺寸采用最小外接截面圆的尺寸。
3)如果内圆柱面的几何公差采用了LMC,最大极限尺寸采用全局最小外接圆柱面的尺寸。最小极限尺寸为局部实际尺寸。虽然标准中,并没说明该类情况,但可以推断。该局部实际尺寸是LP或截面尺寸,如果采用截面尺寸,该截面尺寸为最大内切圆的尺寸。
对于外圆柱面、内球面、外球面,情况类似,见表2所示,不再赘述。
值得注意的是,在GD&T中,宽度的局部实际尺寸只能是两点尺寸LP,因为宽度的截面尺寸没有定义,见图4所示。具体原因,前面已经叙述:截面尺寸要提取2D提取组成要素,需要构造相交平面,相交平面需要和spine垂直,但宽度的spine是个曲面,无法构造相交平面。GPS中,这个问题是不存在的。这是由内部的游戏规则决定的。
图4 ASME Y14.5.1章节2.3.3.3
我们再看一个例子,如图5所示,该尺寸公差采用包容原则,标注了CF,说明是连续要素。根据上面的分析,最大极限尺寸采用了全局最小外接圆柱面尺寸,而最小极限尺寸的类型为局部实际尺寸。
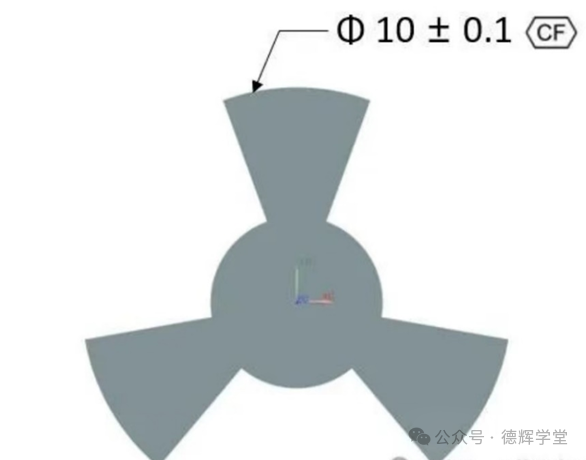
图5 连续要素的尺寸标注
本例特殊之处是:由于存在缺口,相对点对是无法构造的(即垂直于spine的构造线,与实际轮廓相交后,只有一个交点),因此LP是不存在的。
标准对这种情况有明确的说明,如图6所示,因此,只能采用截面尺寸,即最大内切截面圆的尺寸。(该例中截面为三段圆弧,可以共同构成尺寸要素,因为任意一段缺口对应的圆心角小于180度,最大内切圆是存在的。但任意一段单独的圆弧不能构成尺寸要素,具体分析见后文中图9、图10的解释)。

图6 ASME Y14.5.1章节2.3.4
最后,有的小伙伴,会提出这样的疑问:三坐标对于这种有缺口的连续要素,同样能计算出LP。不排除,随着技术的发展,软件内部通过某种规则重构出那个缺失的点对,但其可信度肯定大打折扣,测量不确定度肯定很大,因为这不符合GD&T标准规范。
3.2 不规则尺寸要素是否可以标注尺寸公差?
到底不规则尺寸要素能不能标注尺寸公差?在ASME14.5.1和ASME14.5中,如图7所示,规定规则1#(即包容要求)仅适用于规则尺寸要素。


图7 ASME Y14.5.1章节2.3.6与ASME Y14.5章节5.8
同时,ASME Y14.5的3.35.1中,如图8,不规则尺寸要素的定义中,不规则尺寸要素可以直接标注公差。这里看似有点矛盾。

图8 ASME Y14.5章节3.35.1
标准中,并未给出详细的说明,在此,给出个人见解,权当是抛砖引玉,欢迎吐槽。不规则尺寸要素,能不能标注尺寸公差,取决于被测要素是否存在全局尺寸和局部尺寸。如果两者之一不存在,肯定尺寸公差无法应用包容要求。现将不适合标注尺寸公差的情况分类:
1)全局尺寸不存在
举一个最简单的例子,如一个圆弧(圆周角小于180度),其最大内切圆或最小外接圆是不存在的。如图9所示,内切圆1的半径增大,最后变成内切圆2,还可以无限继续增大下去。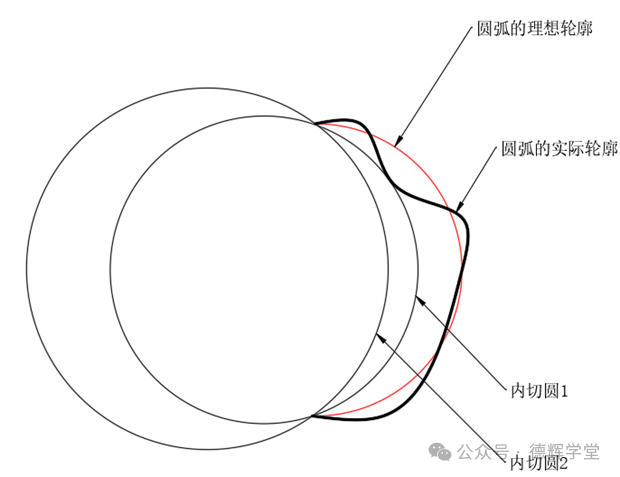
图9 非尺寸要素(不完整圆)
最大内切圆的判别条件是:实际轮廓和内切圆的接触点,构成锐角三角形,如图10所示。这就要求,圆弧缺口对应的圆心角要小于180度。这样的圆弧才是尺寸要素。
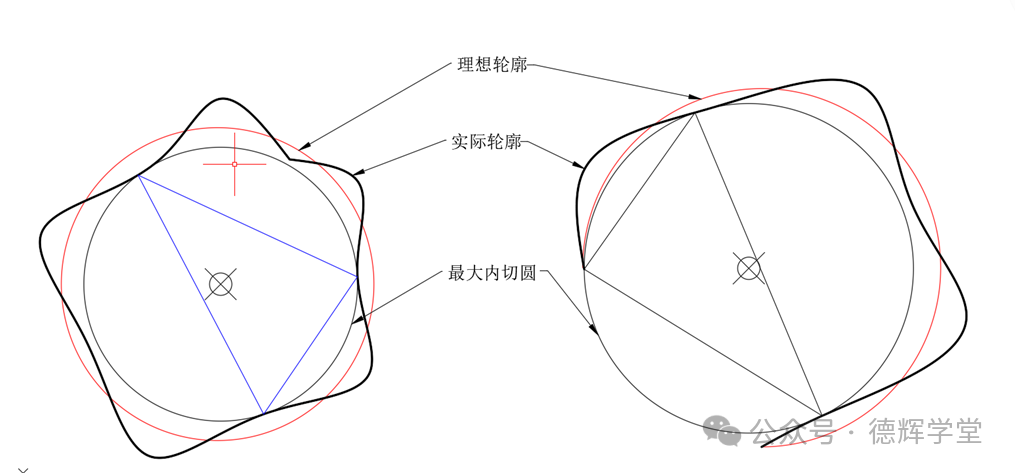
图10 最大内切圆的判定
将圆推广到圆柱面,道理也是一样的,圆柱面的缺口对应的圆周角要小于180度(当然判别条件更复杂,最大内切圆柱面和实际轮廓有5个接触点,是一个四维空间的凸包问题,感兴趣的小伙伴,可以阅读熊有伦院士的《精密测量的数学方法》),此时的圆柱面才是尺寸要素,才具有全局尺寸(即存在最大内切尺寸或最小外接尺寸)。
2)局部实际尺寸不存在的情况
如图11所示,该图是标准ASME Y14.5中非尺寸要素的范例,三段半圆柱面构成非规则尺寸要素,其全局最大内切圆柱面是存在的。但局部尺寸不存在,首先,三段半圆柱体是不存在LP的,因为,找不到相对点对(或者只有边沿那里可以找到相对点对,计算的有效性大打折扣)。第二,每一个截面均为半圆,半圆属于非尺寸要素,其最大内切圆是不存在的。因此,局部实际尺寸处于失控的状态。因此,标准中,仅标注了轮廓度控制其尺寸,而没有标注尺寸公差(应用独立要求和包容要求的尺寸公差均不能标注)。
图11 非尺寸要素的图例1
题外话,图11中的任意两段半圆柱面构成的要素,均属于非尺寸要素,因为全局最大内切圆柱面不存在,大家可以想象一下,一个理想的外圆柱与之配合,慢慢增大外圆柱面的直径,两段半圆柱面是无法约束住外圆柱面的,外圆柱面的直径可以一直增大。同样,算法上,也是无法计算出最大的内切圆柱面。
第二个实例,见图12,基准要素A属于不规则尺寸要素,局部尺寸不存在,相对点对不存在,相对点对不存在,就无法构造spine,没有spine也就没有截面尺寸了。因此,不适合标注尺寸公差(应用独立要求和包容要求的尺寸公差均不能标注)。同样,ASME标准中,该要素标注的是轮廓度公差。
最后一个问题:ASME Y14.5给出非规则尺寸要素的定义时,为什么非规则尺寸要素可以直接标注公差?具体的深层含义,不是太理解,只能揣测一下那些专家的想法:如图11、12这样的非规则尺寸要素,如果通过注,表明最大极限尺寸采用全局最小外接尺寸,最小极限尺寸采用全局最大内切尺寸,这样也是可以的。目前,GD&T推荐的尺寸公差标注,即满足包容要求或独立要求的尺寸公差,是不能标注在图11、12上,但客户或者设计工程师可以指定极限尺寸的类型。
虽然,GPS中没有定义非规则尺寸要素,但是,根据GPS的标注规则,是可以对非规则尺寸要素标注尺寸公差的。标准委员会的专家们,是不是有完善GD&T尺寸公差标注规范的计划那?以便接轨GPS丰富的尺寸公差标注方法?
这也提醒各位搞测量的小伙伴,如果遇到客户或设计工程师在非尺寸要素或非规则尺寸要素上,标注尺寸公差时,一定要问清楚,极限尺寸的尺寸类型是什么。如图9中的非尺寸要素,虽然LP、最大内切尺寸或最大外接尺寸不存在,但是存在最小二乘尺寸和最小区域尺寸,如果客户强行标注尺寸公差,但尺寸类型是最小二乘尺寸或最小区域尺寸,未尝不可,毕竟客户是老大!
【总结】
1、本文总结了ASME中,局部实际尺寸的生成过程,并总结了与GPS的局部尺寸的异同。
2、在ASME Y14.5中,给出了两种局部实际尺寸。大多数工程师,可能只对LP较熟悉,而忽略了截面尺寸。在某些尺寸要素中,LP是不存在的,只能测量截面尺寸。另外,截面尺寸分为两种,我们对两者应用的场合,进行了总结,见表2。
3、最后总结了不规则尺寸要素不能标注尺寸公差的原因。在GD&T中,非规则尺寸要素不能标注尺寸公差,主要是由其原有的游戏规则决定的。
【作者简介】
陈磊磊(网名转角黎明),桂林电子科技大学机电工程学院,专任教师,在读博士,研究方向:基于GPS/GD&T的几何产品误差的测量、几何产品公差的智能设计,联系方式:15676308162
