上期文章的最后，我们出了一道思考题：

    【思考题】在一些汽车钣金零件上，有些过线孔，孔的孔径要求比较严格，孔的位置度要求比较松，见如下标注，请问位置度能用检具检测吗？如果可以，检具该如何设计？

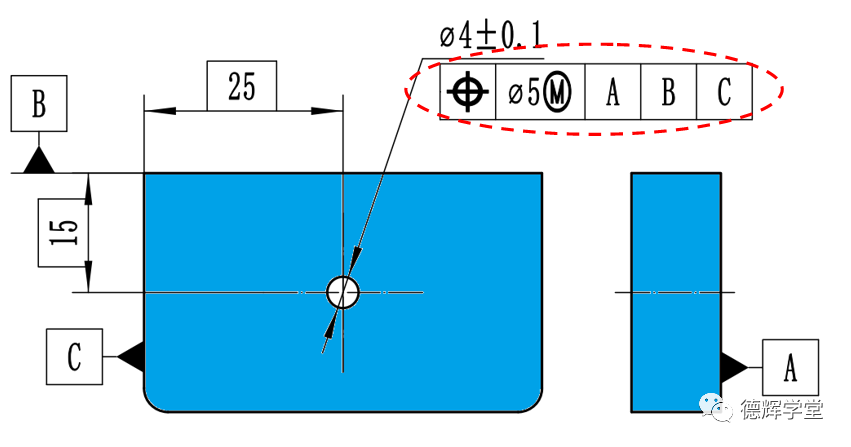
图1 孔的位置度如何设计检具.

     图1中，该零件孔的位置度比尺寸还大，这个时候我们该如何设计检具呢？

     如果按照常规的检具设计思路，我们第一步是计算检测销的直径。

     再根据前几期文章中，我们介绍的知识点，必须要用到MMVB的大小来确定检测销的直径，其中，MMVB的计算公式为：

MMVB=MMC-位置度

     图1的诡异之处在于，MMVB是负数：

MMVB=3.9-5=-1.1

     这个时候，检具检测销，检具的方案该如何确定呢？

     本期我们就来仔细探讨这个话题，老八股，本期文章分三个小节：

1.      1.  位置度采用M圈后的特点;

2.      2.  伪实效边界MMVB*和扩实效边界MMVB+;

3.      3.  基于MMVB+的特点设计检具.

   
   

   
   

4.      废话少说，直接开始吧。

1.      这个话题，在德辉学堂往期文章中，我们反复介绍过，任何一个形位公差一旦采用了最大实体要求后，最大的特点是：

   
   

2.      1. 内特征（Internal Feature），比如，孔，槽这类“母”的特征，内边界（IB）保持不变；

3. 
   

        2. 外特征（External Feature），比如，轴，板这类“公”的特征，外边界(OB)保持不变；

     至于什么是边界，我假设您还记得下边这个图片（图2），具体我不解释了（没有看过往期文章的小伙伴，点击本文最后的链接）。

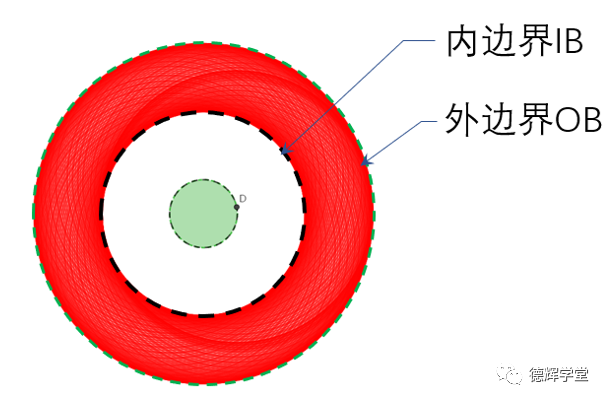
图2 随机运动的孔形成了边界

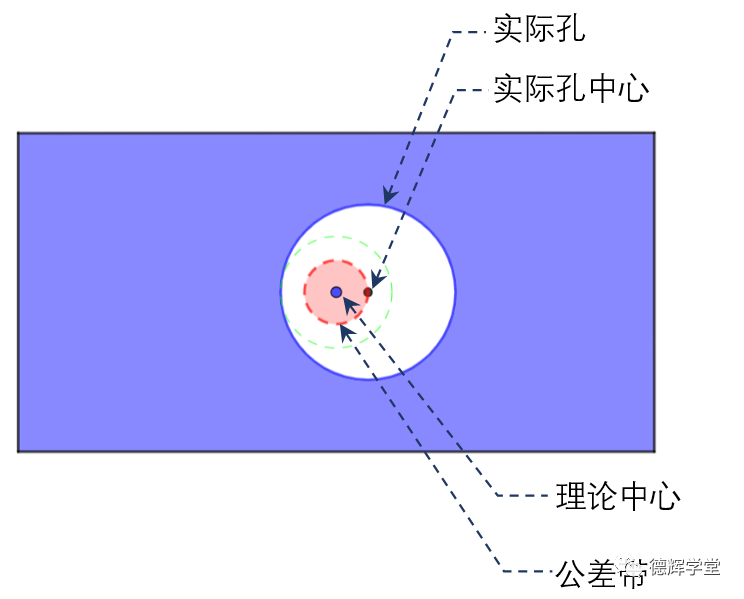
图3 孔轴线和公差带之间的关系

     同样的套路，我们假设孔的中心刚好在公差带的外边缘游走，这样一动，就会形成一个固定不变的内边界IB，见动画1.

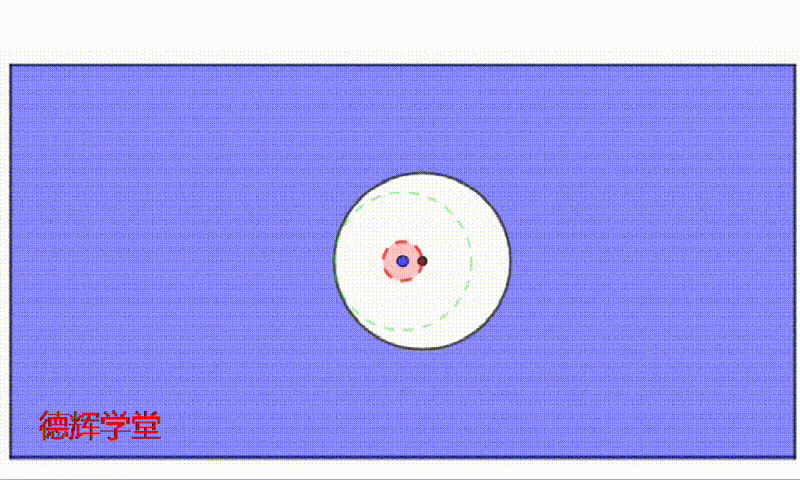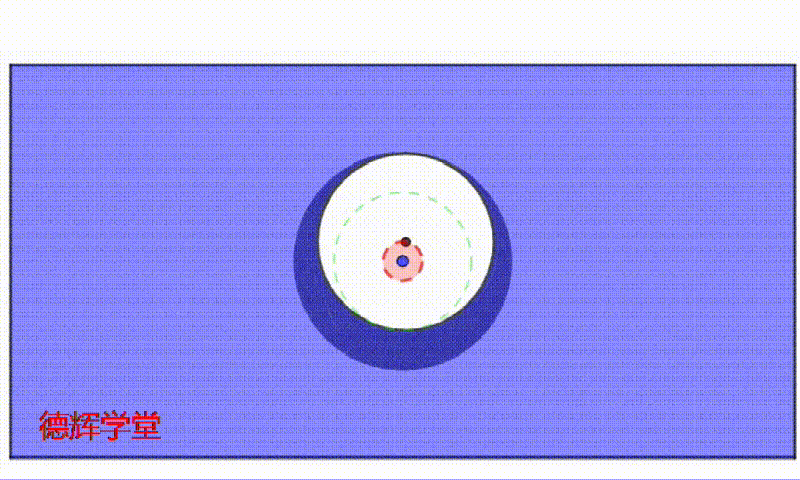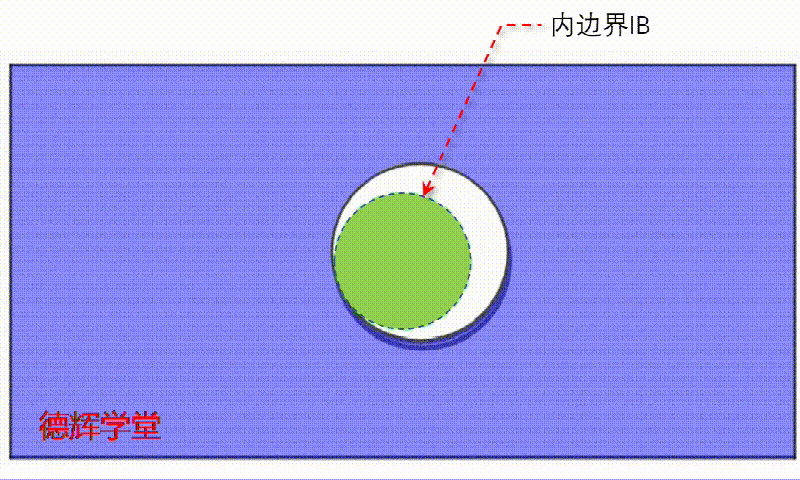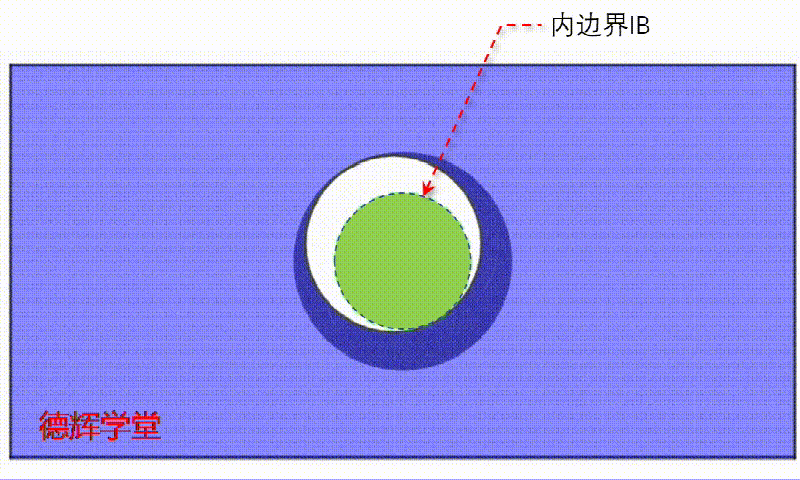
动画1 内边界的形成

     注意，动画1中，绿色的区域为内边界IB， 它里边一定是空心的。

     而且，我们在往期文章中，也强调了，几何公差加了最大实体要求后（带M圈），公差带的大小会随着孔的大小变化而变化。

     比如，关于孔的要求如下（见图4），对应的实际孔径，补偿（Bonus）,允许位置度和内边界的关系如下：

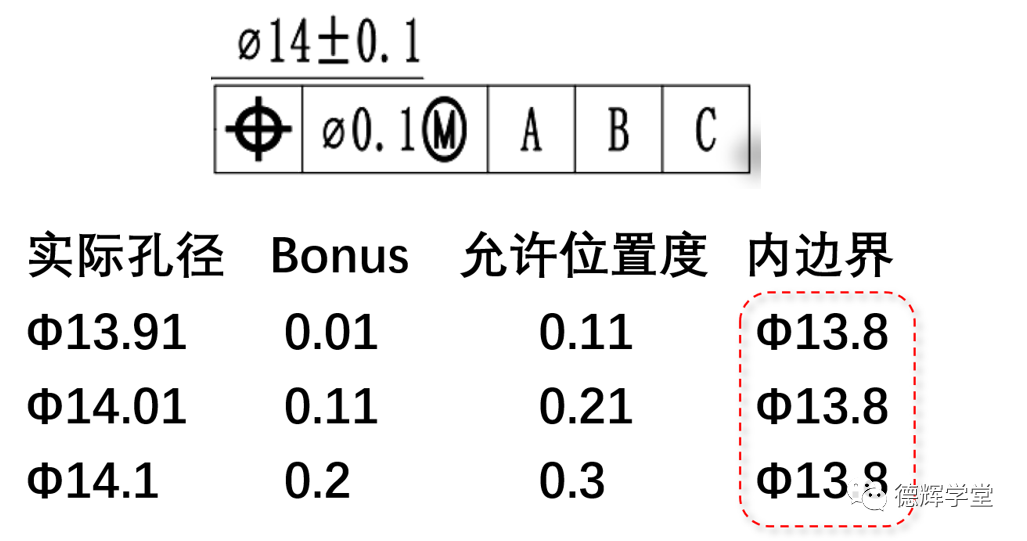
图4 实际孔径和允许位置度的变化规律

     上面的信息，我们以往都提到过，请大家仔细观察上面的规律，这里不再赘述。

     这里唯一要强调的是，M圈的游戏规则决定了补偿（Bonus）的大小（我假设您还记得Bonus的计算公式），补偿的存在，导致了该孔的内边界IB，不管孔的大小如何，最小的IB一定保持不变。

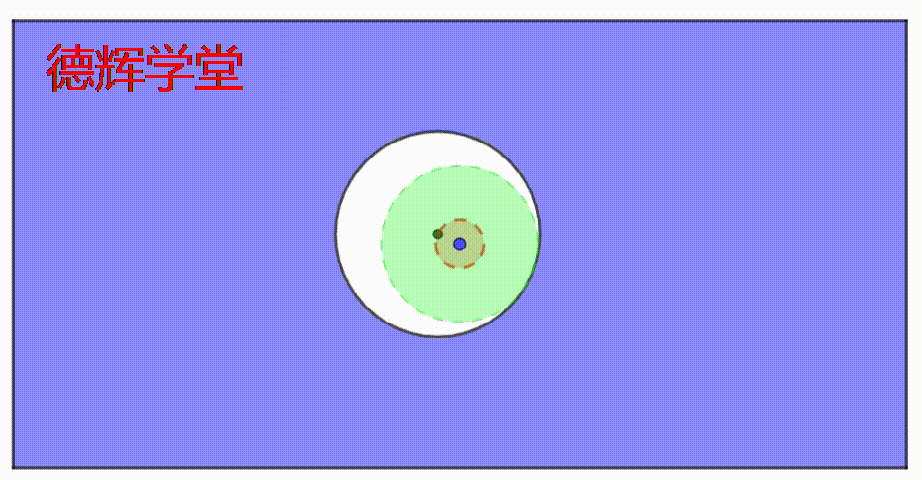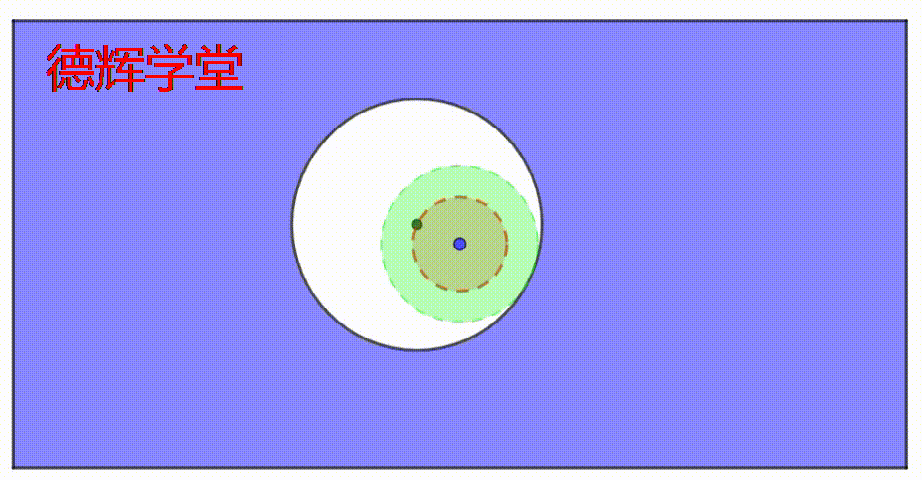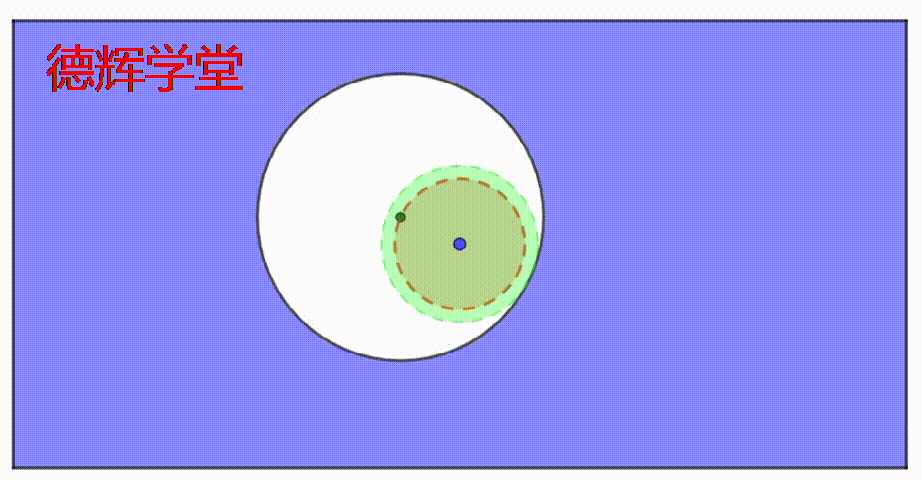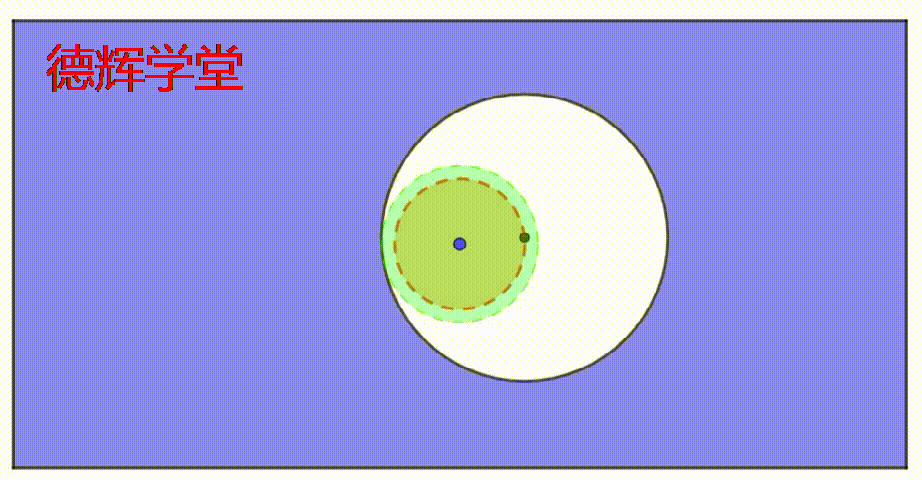
动画2 固定不变的内边界IB

     如果您耐心看完上面的动画，您会感受到，不管孔径和公差带怎么“联动”，但是绿色区域的大小却固定不变。

     也就是说，不管孔的大小和公差带的大小怎么联动，在孔的内部一定有一个固定直径的空间，它内部是绝对空心的。

     保证这个空心的绿色区域大小不变，这个正是制定M圈游戏规则的底层逻辑所关注的。

     动画2中，绿色空间永远空心，基于这个特点，所以要检测该空间是否还存在（内部不能有任何材料），检具设计的时候，人们只要拿一根和该空间大小一样的反特征，一根实心的销子去插，能插进去就算合格（表明空间还在），见动画3.

动画3 用检具销检测内边界

     逻辑梳理好后，我们再来看看本期文章要解决的问题。

2.伪实效边界MMVB*和扩实效边界MMVB+

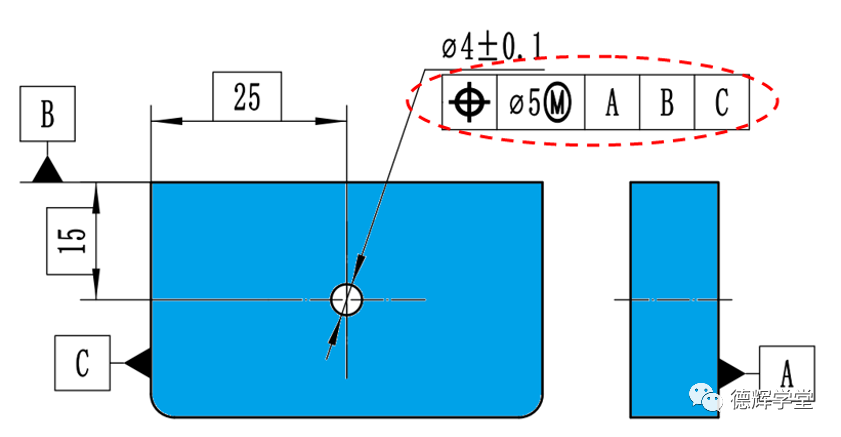
图5 本期题目

     见图5， 图5中最大的特点是，位置度比尺寸还要大。

     如果我们用常用公式计算：

            =3.9-5

            =-1.1

     会发现这个MMVB_H 是一个负值，这是什么意思？

     这里我们做个定义，MMVB大小为负值时，它也是个边界，叫“伪最大实体实效边界”,简称“伪实效边界” ，用MMVB*表示。

     这个MMVB*具备什么特点呢？

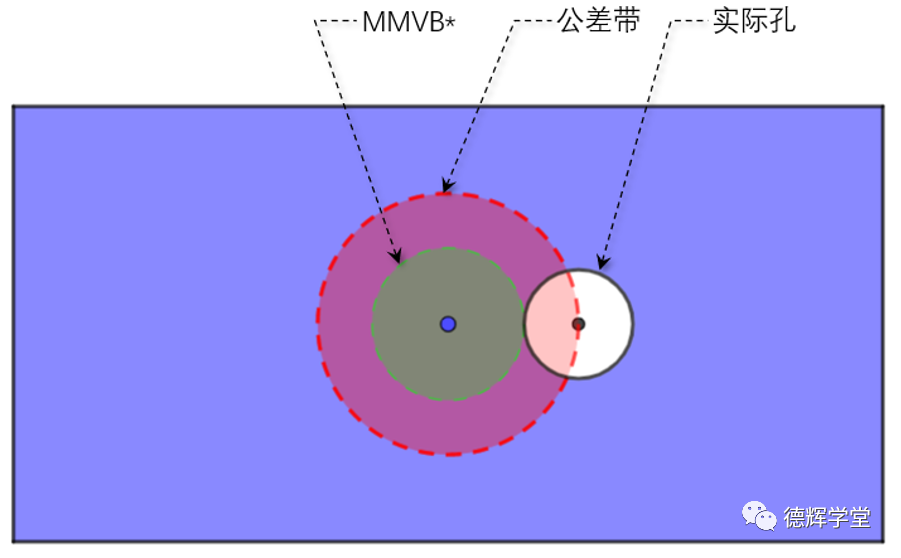
图6 伪实效边界的产生

     见图6， 红色的区域表示公差带（很大），白色的是实际孔（很小），注意，这个绿色的区域就是伪实效边界。

     还是来看看动画吧，动画中结合了最大实体的游戏规则，和边界理论的特点，希望大家仔细观察。

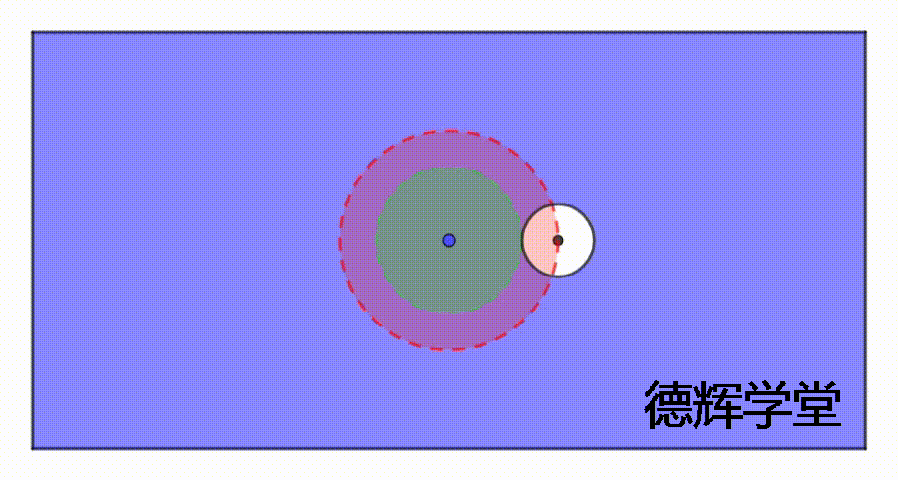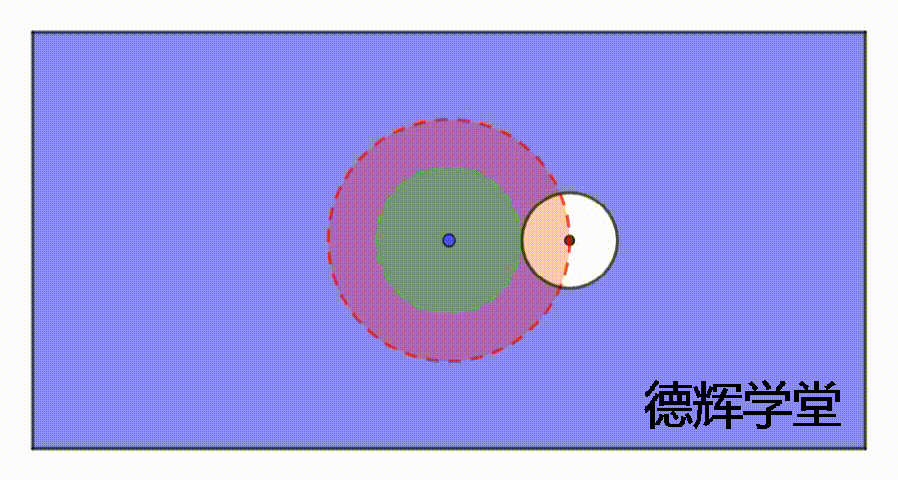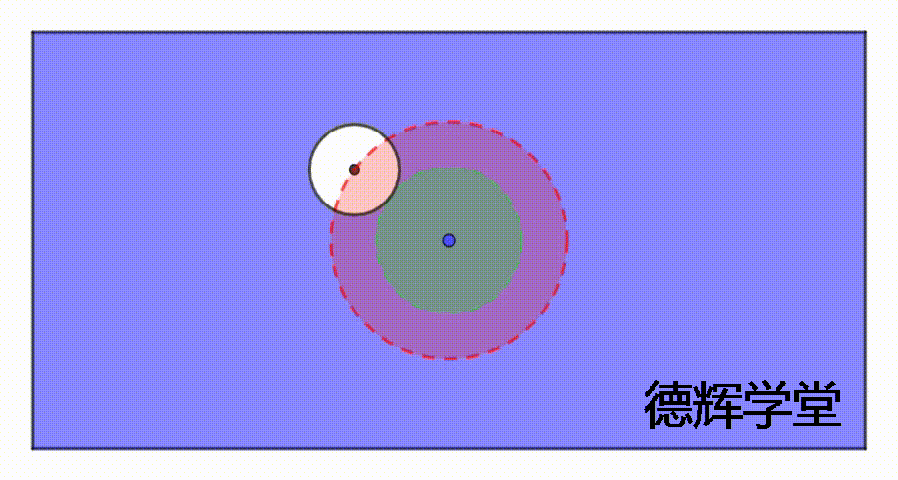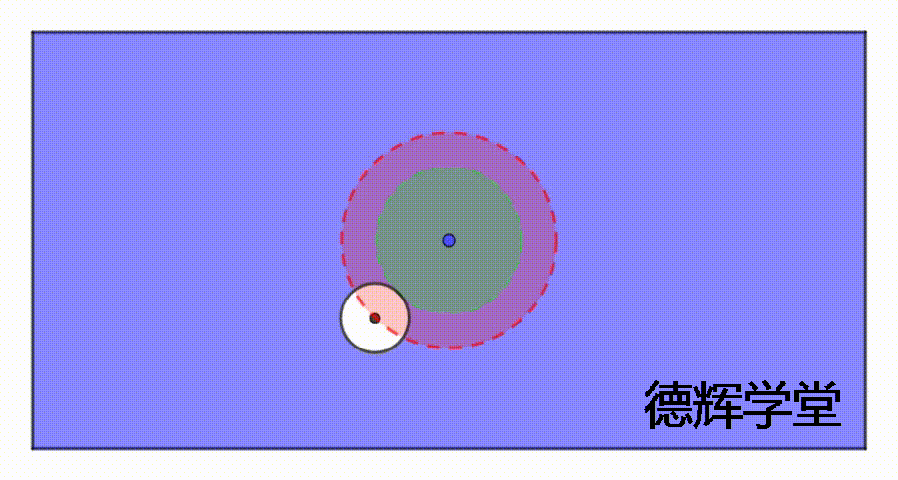
动画4 伪实效边界的产生

     注意，动画4中，我们只是展示了孔在极限位置（孔中心刚好在公差带边缘）所形成的固定边界。我们用表格观察规律的话，其实也可以列出来，它的“内边界”不变。

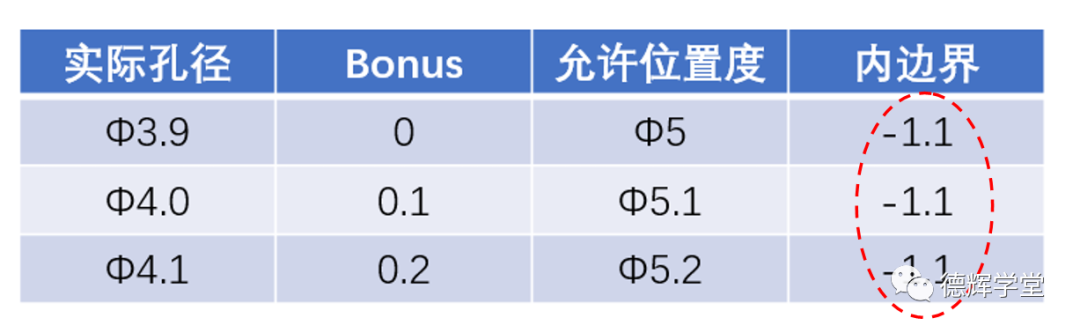
图7 固定不变的“内边界”

     这个结果为负数的内边界，我们叫它“伪内边界”，同样，用IB*表示。

     位置度加了M圈后，如果位置度比孔径（MMC时的孔径）还大，它就会形成一个固定不变的“伪内边界”，同时也是“伪实效边界”，即:

IB*=MMVB*

     这个MMVB*的直径大小该怎么计算呢？废话少说，直接观察下图吧：

图8 MMVB*的计算方法

     根据图8中显示的几何关系，再结合图7中表格的数据，不难得出：

                   =2(R_T-R_H)

                   =2R_T-2R_H

                   =位置度-MMC           （1）

     其中：

1.      1.  R*是伪实效边界的半径；

2.      2.  R_T是位置度公差带的半径；

3.      3.  R_H是孔径(处于MMC时的半径)；

备注：

1. 公式（1）中MMVB*同时也是表示伪实效边界的直径大小，各位小伙伴注意；

2. 如果要了解详细的推导过程，建议看德辉学堂公众号的另外一篇文章《检具检测销的直径如何设计》；

     注意公式（1），是不是刚好和常规MMVB的计算公式反个号？

     我们在讨论边界理论的时候绝大部分情况是孔径大，位置度小，这种情况下形成的内边界IB或实效边界MMVB， 是一个“真边界”。还记得它们的计算公式么？

     前边反复强调过，当孔径（MMC）大于位置度时，几何公差和位置公差形成的内边界，里边一定是没有材料的，是空心的。

图9 “空心”的内边界

     而当位置度大于孔径（MMC）的时候，产生的边界是伪边界，这个伪内边界IB*的内部，可不是绝对空心的哦，里边完全有可能有材料！

     我们看另外一个动画，来观察伪实效边界的内部，这个动画模拟了孔在大公差带里，随机运动的过程。

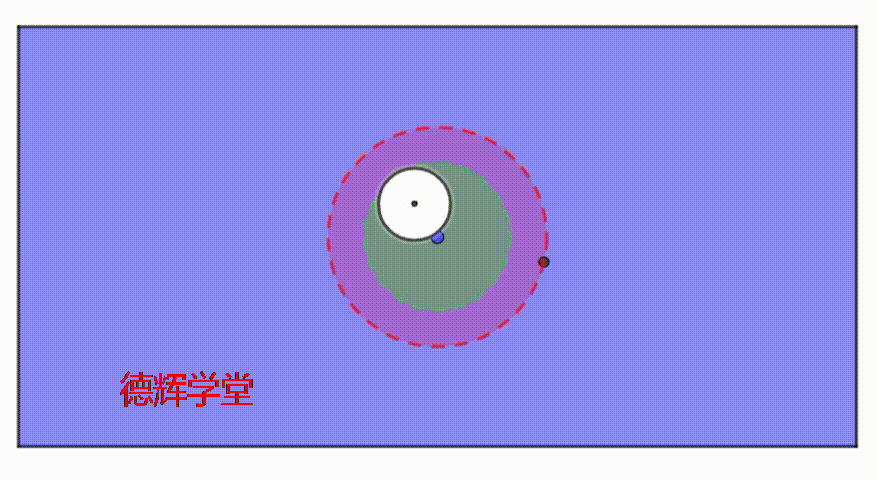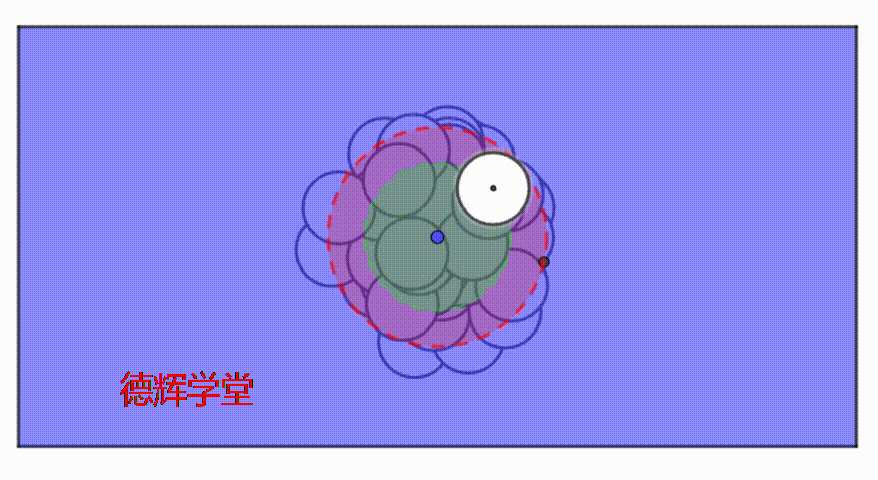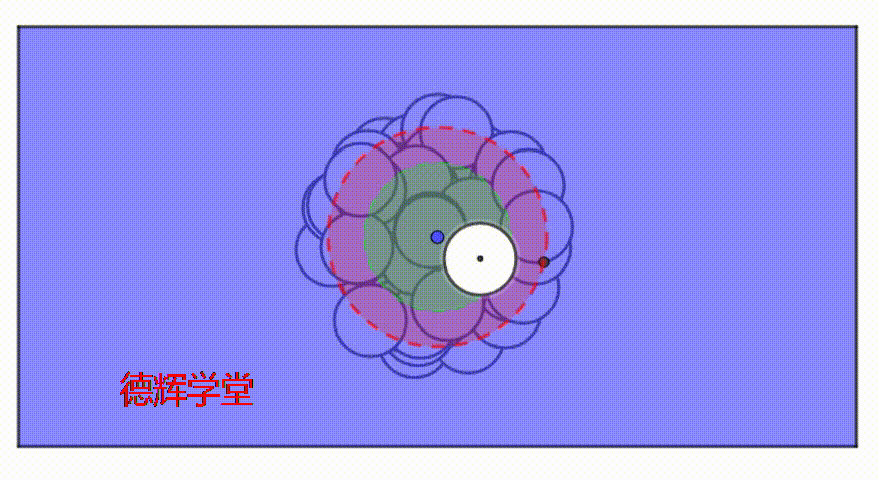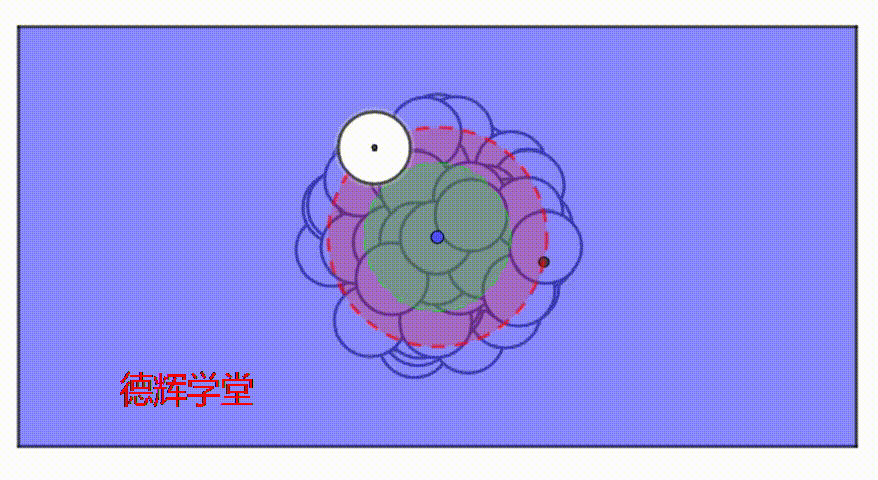
动画5 孔在公差带里随机运动

     大家仔细观察动画5，这个孔的在伪实效边界（MMVB*）的内外随机运动，也就是说，动画5中，不可能存在一个固定的绝对空心的空间。

     这下麻烦了，我们的目的是要设计一个检具，没有一个确定的空间，我们如何设计检具呢？

     我们先把伪边界用绿色的虚线加粗，大家再仔细观察下边这个动画。

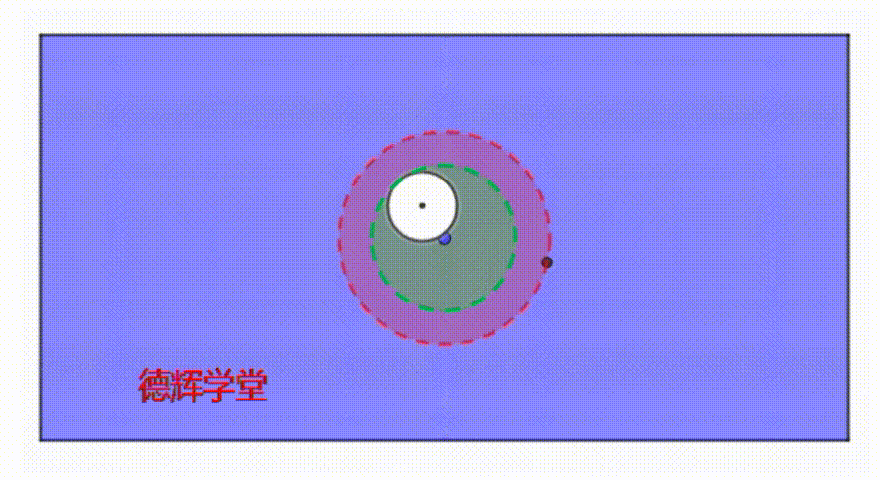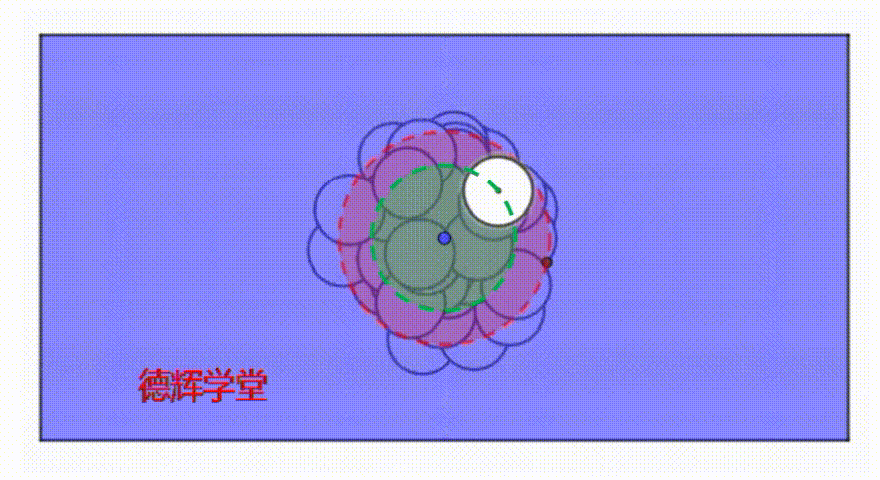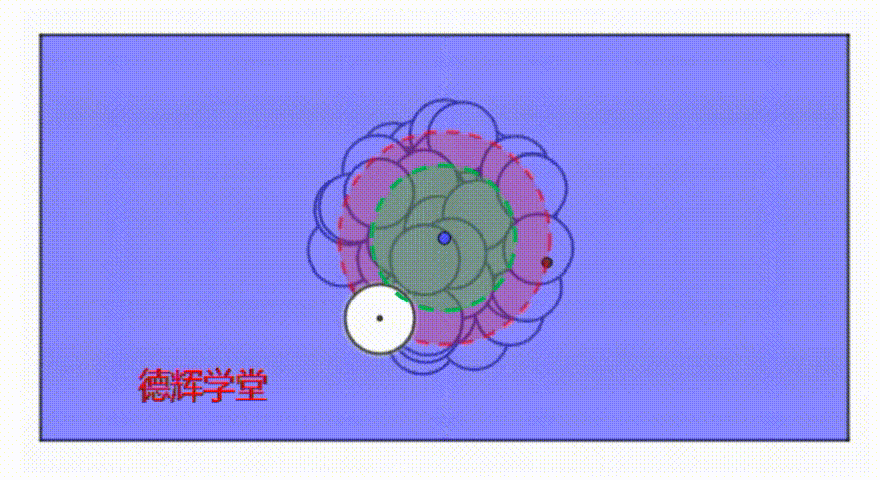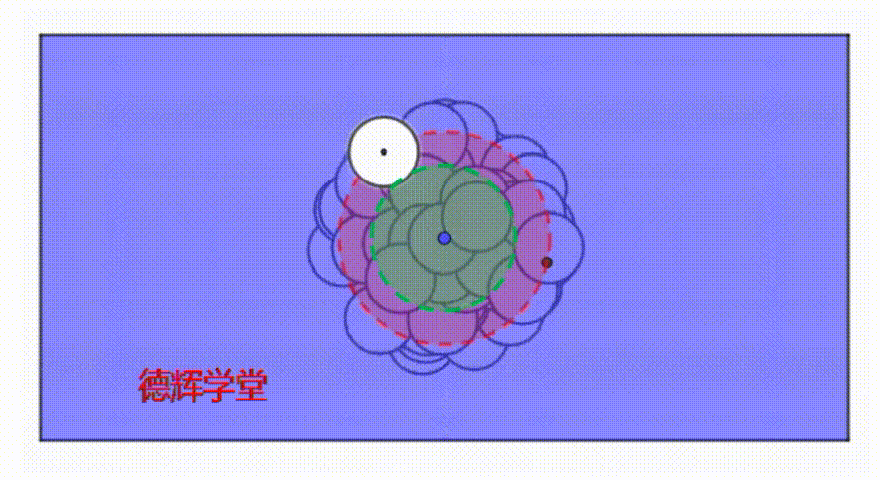
动画6 孔在公差带里运动的特点

     大家仔细观察动画6，当孔在运动时，伪实效边界MMVB*和白色的孔H，有没有可以描述的特点？

     心细的小伙伴可能已经看出来了，伪实效边界也有自己的特点，那就是：

     MMVB*和白色孔H之间总有交集（相切也是相交）！

     我们用数学公式来描述吧，把MMVB*的内部区域看成一个集合，把孔H的内部空心区域也看成一个集合, 那么上面黑体字的一段话，可以表述成：

MMVB* ∩ H ≥ 0

     这句话从直观上怎么理解呢？我们假设伪实效边界是一个空心的大孔，那么他和实际的被测小孔之间，绝大部分情况下，一定有一个公共空间（重叠区域），最坏的情况下是边缘相切，公共空间的大小刚好是0。

     为什么罗里吧嗦的说这么多？因为这涉及到我们检具的逻辑。

     再往下走，我们再把MMVB*的直径人为扩大2mm, 也就是半径扩大1mm, 形成另外一个比MMVB*大一点的圈圈。

     我们再取个名字，将MMVB*扩大后的这个新圈圈叫扩实效边界，用MMVB+表示（取了这么多名字，是为了后边好描述），它们具有下面关系：

MMVB+ = MMVB*+2

     这个MMVB+有什么意义呢？注意，这个扩大后的空间MMVB+和MMVB*不同，它和被测白孔之间，最少最少有1毫米宽度的交集（暂时用1表示）！

MMVB* ∩ H ≥ 1

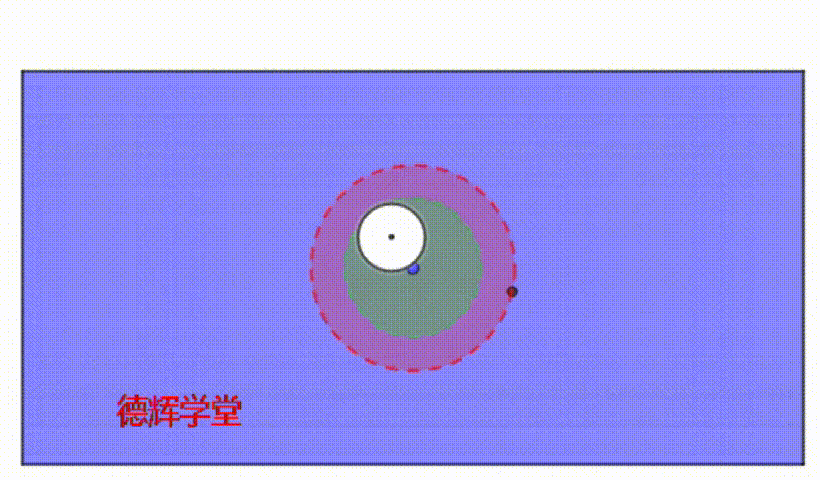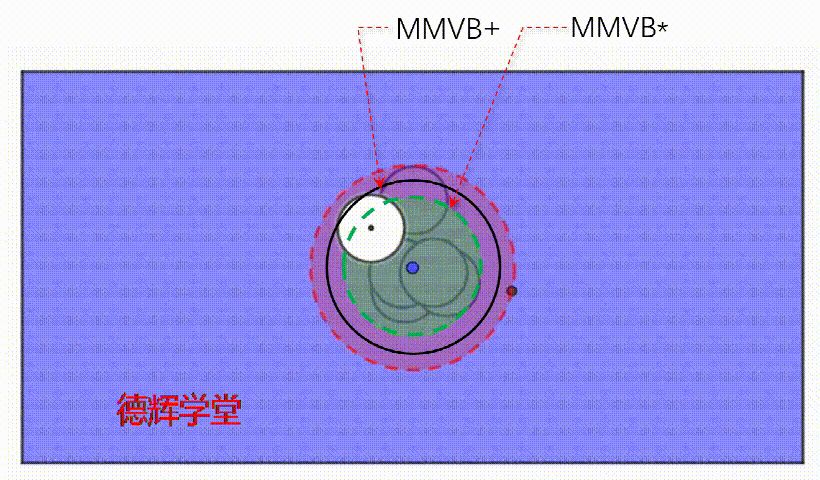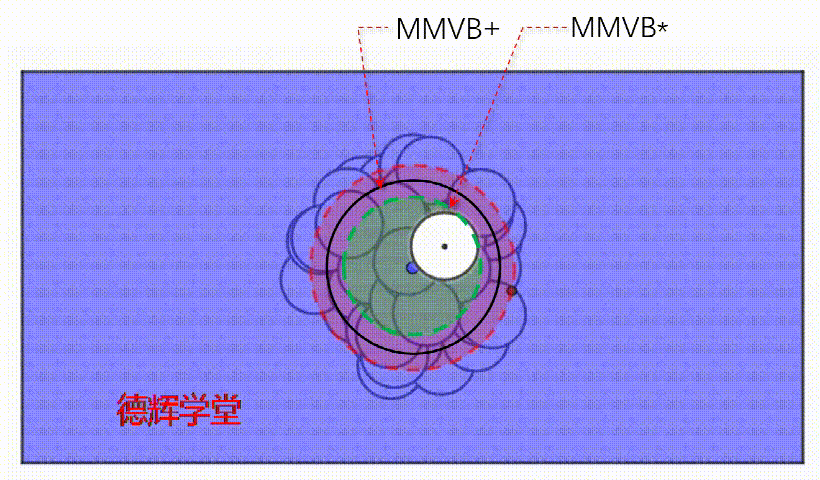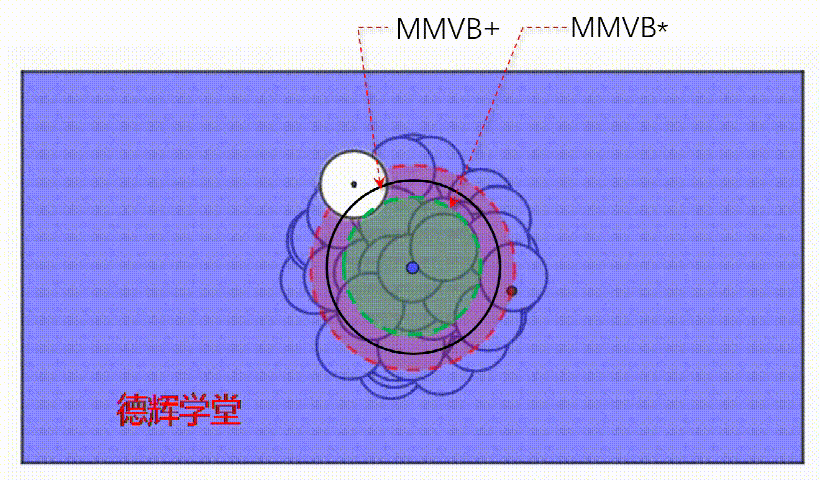
动画7 被测孔和MMVB+的交集

     我们为什么如此在意这个交集？因为可以做检具啊！

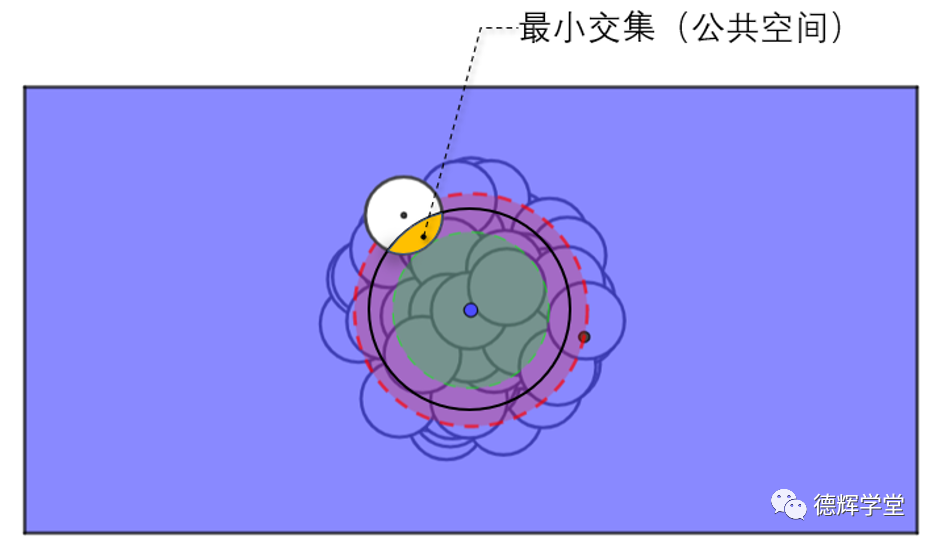
图10 MMVB+和被测孔的交集

     还是和MMVB*的假设一样，MMVB+我们也可以把它看成是一个空心的空间，图10就显示了，白色圈圈的被测孔，在位置度最坏的情况下，和MMVB+(图10中的黑色圈圈)的最小区域交集，也就是图10中的黄色区域。

     为什么要把MMVB+“看成”一个空心的空间呢？

     因为好做检具，第三节大家会体会到。

     注意，图10中，黄色区域是空心的空间，这个空间在半径方向上的最大宽度是1mm（前面说过，黑色圈圈是半径扩大了1mm）。

图:11 在交集里插入销子

     显然，在随机变化的过程中，图11中的白色圈圈（被测孔H），也有可能全部沦陷到黑色圈圈里的。

     那也没有关系，图11中1mm红色的销子同样能够插进去。

     经过我们的分析，做检具是不是有戏了？

3. 基于MMVB+的特点设计检具

     好了，前面叽叽歪歪了一大堆，开始进入真正的主题。

     关于检具的原理和测量方案，直接用动画展示，希望大家从头到尾把动画看完：

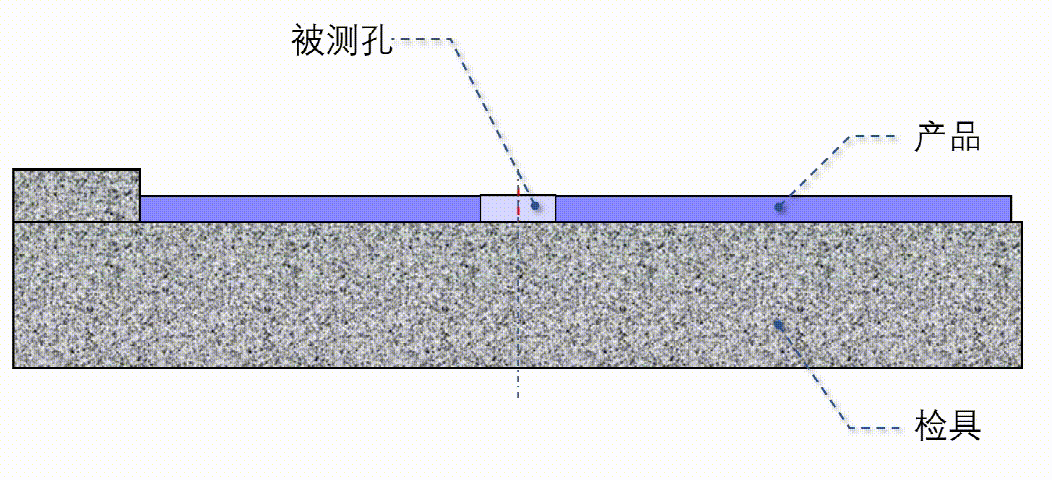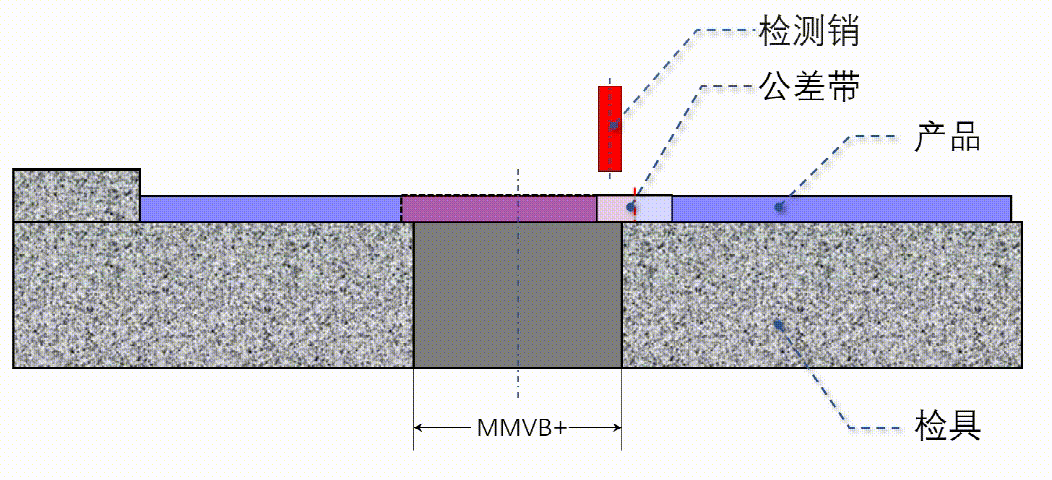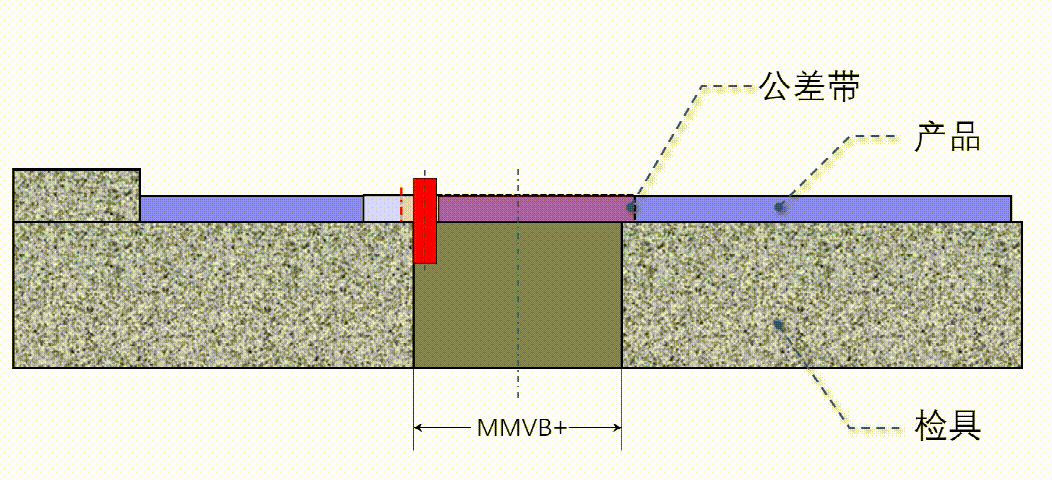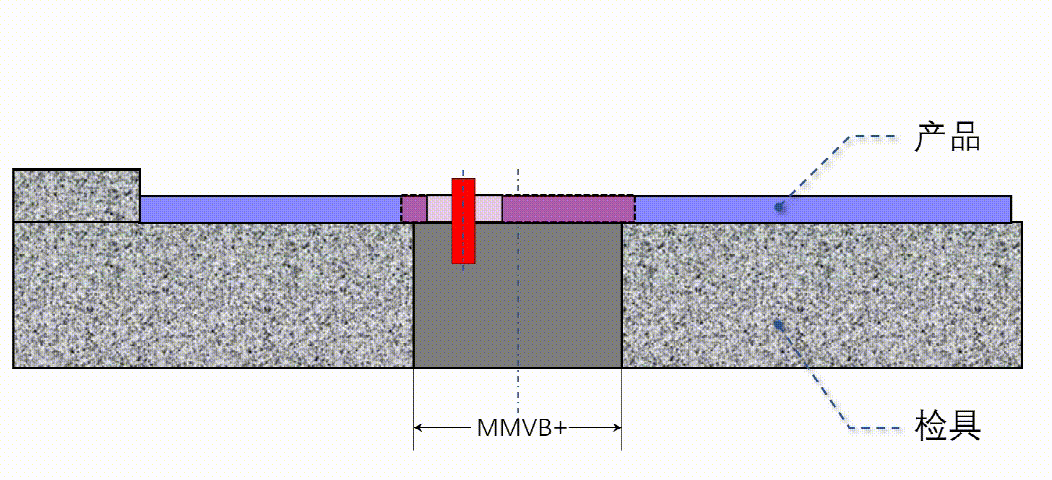
动画8 检具设计方案

     所有的描述都在动画8里。

     检具底座，在相对于基准的理论位置（被测孔的理论中心）上，做一个空心的孔，模拟扩实效边界，直径为MMVB+, 假设检测销的直径为d, 那么MMVB+的计算公式为:

MMVB+ = MMVB* +2d

     将被测产品放在检具上，用相应的基准块定位好后，再像动画8一样，用红色的检测销去插被测孔，只要红色的检测销能够插进被测孔，就说明该被测孔的实际位置一定在公差带范围内。

     欧了。

     我们把刚刚的思路再重新理一遍：

     当孔的位置度比孔径还要大，若要做检具，检具的方案见动画8，至于计算过程，如下：

1.      1.  先确定检测销的直径d, 推荐取1-3mm，自己取，基于强度和制造难易选择；

2.      2.  计算伪实效边界MMVB*:

     3.     再确定扩实效边界MMVB+:

MMVB+ = MMVB* + 2d

     还是举个例子吧，就上期文章的问题而言，图纸如下：

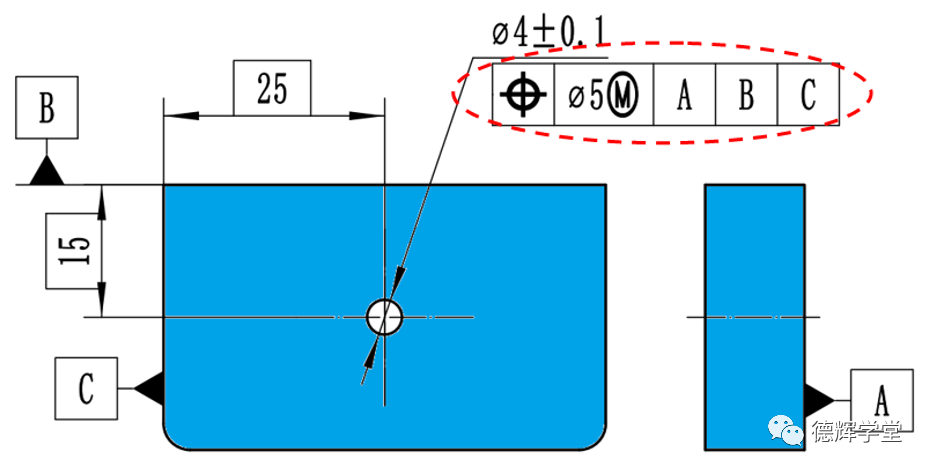
图12 上期问题

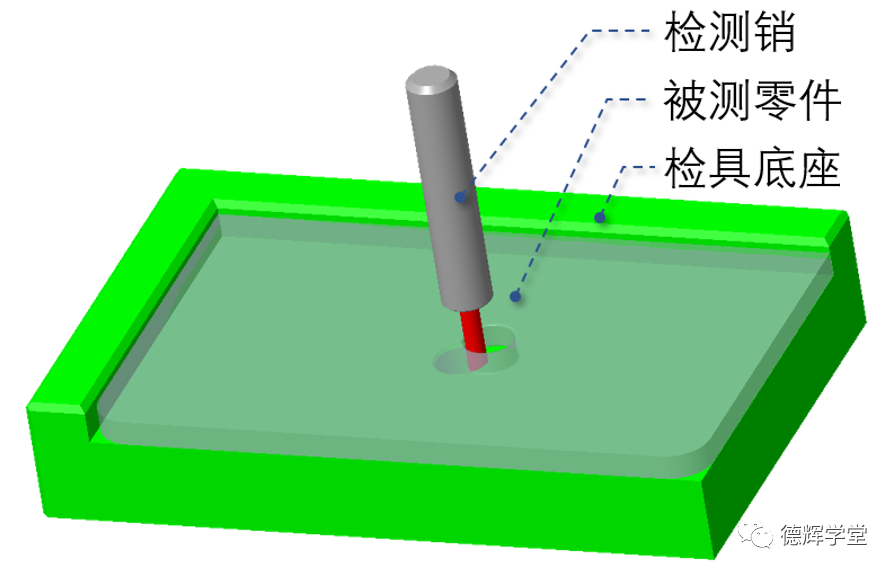
图13 零件和检具方案

     计算过程：

1.      1.     先确定检测销（图13中红色销子）直径，我们自己取d=1.5mm；

2.      2.     计算MMVB*:

     3. 计算MMVB+:

     检具的具体尺寸见图14：

图14 检具的相关尺寸

【内容回顾】

     本期文章探讨了当位置度比孔径还大的时候，如何设计检具。为了理顺后边的逻辑，文章分了3个小节来探讨：

     文章第一节，文章还是和小伙伴们快速回顾了当位置度采用M圈后，内外边界的特点。重点强调了因为内边界IB不变，而且是空心的，所以，常规检具的方案是直接插入检测销；

     文章第二节，探讨了当位置度比孔径大的时候，边界是负的，引出了伪实效边界MMVB*的概念，同时也延伸到扩实效边界MMVB+, 强调了被测孔和MMVB+最少有一部分交集，这个是设计检具的关键；

     文章最后，是基于MMVB+和被测孔之间一定有最小交集这个特点，利用最小交集设计检测销，给出了检具的设计方案，以及相关特征尺寸的计算方法。

【后记】

     本期文章属于探讨性质，并非常规的技术普及，文章或许有逻辑漏洞，或许还有更好的办法，欢迎各位小伙伴提出来，或者写成文章给我们，合适的话，我们会发表在德辉学堂公众号上哦。

     需要说明的是，本期文章给的检具方案，比较适用于薄的钣金件，比如汽车钣金的走线孔。对于比较厚的零件，文章中的检具方案是有缺陷的（小伙伴们可以自己思考一下什么缺陷）。

     另外，再深入思考一下，MMVB最大实体实效边界，MMVB*伪最大实体实效边界，以及它们的反特征，检具检测销，之间的关系，从数学的原理上讲（比如基于集合理论），一定有共同点（比如大一统的公式之类的）。

     或者说，我们应该用什么样的数学思维，去思考这类问题？

     遗憾的是，本人数学水平有限，没能把这个共同点给抓出来（文中很多逻辑是通过动画，是凭“感觉”，这种不太严谨的东西来推演的），有兴趣的小伙伴可以思考这个问题，欢迎随时和我沟通哦。

     最后，关于本期问题的提出，位置度比孔径大，如何做检具，最早是尺寸工程爱好者及专家秦悦秦工提出来的问题，我们一起探讨过，后边我在给学员上检具设计课的时候，不少学员也提出来这个话题，最近一次是卡涞科技的李世春李工也提出来同样的问题，这些问题的提出，促成了本期文章的完成，在这里向以上小伙伴表示感谢！

     老套路，文章最后，留一道思考题给您：

【思考题】 已知图纸如下，在加工孔φ4±0.1的时候，我们经过统计发现，25的尺寸服从正态分布（已知平均值u和标准偏差σ），15的尺寸也服从正态分布（已知平均值u和标准偏差σ），那么下图φ5的位置度的实测值服从什么分布呢？我们怎么来要求供应商，要求它的合格率控制在99.9937%范围内呢？

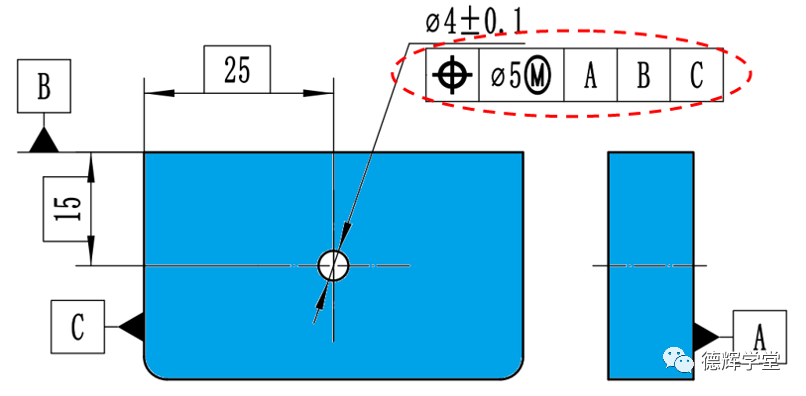
图15 本期文章思考题

     欢迎给我们留言，说说您的思考。

*********完*********