本期文章的第一篇我们探讨了计算T值或者轮廓度所需要的基本数学知识，比如矢量的减法和乘法。

我们先将第一篇介绍的核心内容回顾一下。

1）矢量的减法计算：已知空间坐标中的两点, 点A（x1, y1, z1）和点B（x2, y2, z2），利用矢量的减法，则可以得出矢量AB的坐标为（x2-x1, y2-y1, z2-z1 ），利用这个信息，我们可以得出AB的长度和方向角。

2）投影长度的计算：已知空间坐标中的两点, 点A（x1, y1, z1）和点B（x2, y2, z2），利用矢量的乘法再整理，则可以计算出矢量OB在OA上的投影l OB’l 。投影计算公式为：

lOB’l =（x1*x2+y1*y2+z1*z2）/lOAl 

本期文章的内容就是上期文章所介绍的数学知识点的具体应用，今天，我们将探讨剩下的两个章节。

2. T值的计算原理

3. 带基准轮廓度的计算原理

还没有读上一篇文章的小伙伴，建议先读一读再来看这篇文章。

2. T值的计算原理

当我们用UG或者Croe等3D软件设计好零件的型面，供应商根据3D数模开模具生产出零件，此时我们如果想知道供应商提供的零件的型面和3D数模的型面是否一致的时候，我们就会用到T值（矢量方向偏差）来判断。

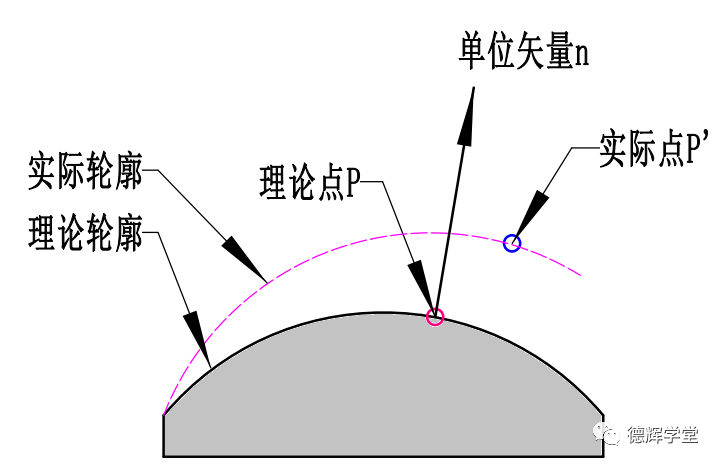
图10 实际轮廓和理论轮廓

如图10所示，通常我们的做法是，在理论轮廓上采一个理论点P（采的点越多越好），然后在实际零件上的同样位置采一个实际点P’, 将实际点P’和理论点P进行比对。此时，我们希望实际点P’和理论点P越近越好（最好重叠），这样就说明供应商做的零件型面的误差就越小。

事实上实际零件的型面和理论3D数模型面一定有偏差，比如图10中的点P’和P就一定不会重叠。那么，我们如何评估这种偏差呢？

很多三坐标软件，都提供了“矢量方向的偏差”这个评估参数，比如PC-DMIS就采用的T值代表矢量方向的偏差。

T值究竟代表什么偏差，它是怎么计算出来的呢？

我们知道，当我们在3D数模上选取了一个理想点P, 我们就会得到2个信息（这些信息是3D数模自带的）：

1. P点的坐标（x1, y1, z1）

      2. 过P点的单位矢量n。

     注意，该单位矢量n的特点是垂直于过P点处的切面（也就是说，单位矢量的方向是P点处的法向），而且方向是从材料里边指向材料外边。当然既然是单位矢量，显然有lnl = 1.（对单位矢量不了解的小伙伴，点击文章最后链接《三坐标中的矢量是干什么用的》）。

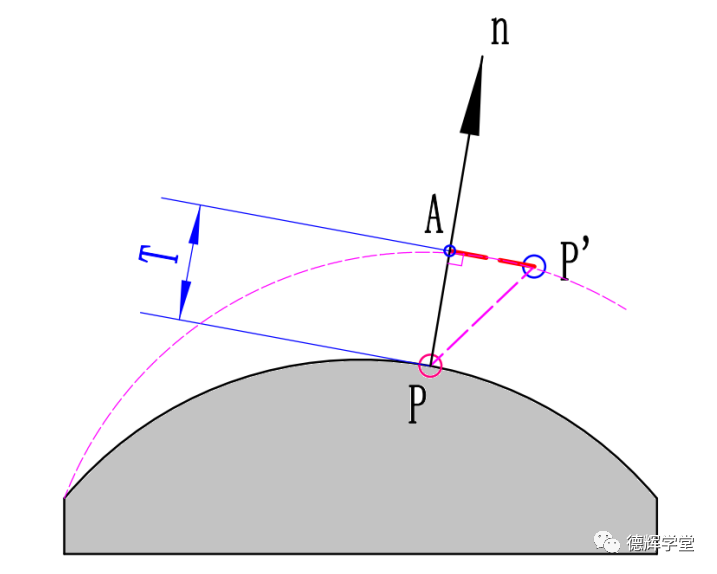
图11 T值的计算原理

见图11，我们过实际点P’作单位矢量n的垂线, 垂足是A。那么线段PA就是矢量PP’在单位矢量n上的投影。

而这个投影就是T值。

也就是说T值，就是理论点和实际点的连线PP'在单位矢量n上的投影（一个分量）！

还记得前面讲的投影公式吗？假设理论点P的坐标是（x1, y1, z1），实际点P’的坐标是（x2, y2, z2）， 那么图11中矢量PP’的坐标则为（x2-x1, y2-y1, z2-z1）。如果测得已知P点处的单位矢量n的坐标为（a, b, c），利用我们前面所推导的公式，则可以得出：

T=lPAl

  = ((x2-x1)*a+(y2-y1)*b+(z2-z1)*c)/lnl

又因为单位矢量n的模为1，即lnl=1， 所以上面的公式可以整理为：

T=lPAl

= ((x2-x1)*a+(y2-y1)*b+(z2-z1)*c)  （10）

注意，公式（10）是计算T值的通用公式，非常重要，大家最好记住。

我们还可以得出一个非常重要的结论，任何一个向量，它和一个单位向量相乘（数量积），其结果就是此向量在该单位向量上的投影！如果得出的结果是正值，投影则和单位向量同向，如果结果是负值，表示投影则和单位向量相反。

和单位向量相乘（数量积）就可以直接得到投影，这就是人们采用单位向量的优势之一吧。

好了，T值的计算方法我们知道了，我们再用PC-DMIS来验证一下。

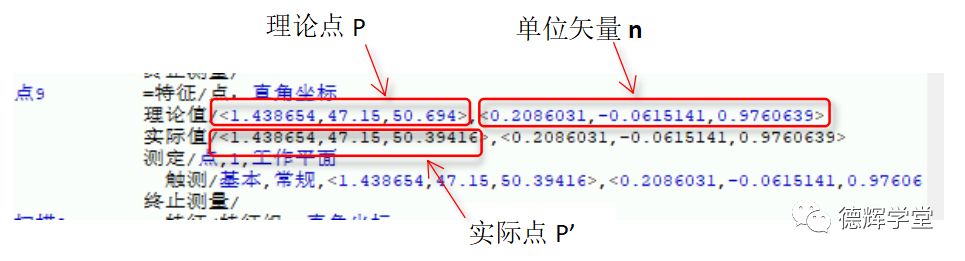
图12 理论点P和实际点P’数据

       图12是PC-DMIS显示的理论点和实际点的原始坐标信息。将图12中的理论数据和实际数据数据输入EXCEL， 用刚刚那个公式（10）计算。计算结果如下：

图13 Excel计算结果

根据公式（10）的计算结果，我们可以得出实际点在矢量方向的偏差， 即T值为-0.292663。

     再来看看PC-DMIS的报告。

图14 PC-DMIS的计算结果

从图13和图14可以看出，Excel的计算结果和PC-DMIS的结算结果是相同的，表明PC-DMIS也是采用同样的计算方法。而且从结果还可以看出，比起理论点P，实际点P'实际上是偏低的，低于理论表面（和单位矢量的方向相反）。如果需要修模的话，应该让零件表面在该点处加材料来修正。

3. 轮廓度的计算原理

理解了T值的计算原理，再来理解轮廓度的计算原理就非常容易了。因为计算轮廓度误差实际上就是计算很多测量点的T值，无非我们需要找到T值最大的那个点。

已知零件标注如图15所示，在计算轮廓度误差的时候该如何计算呢？

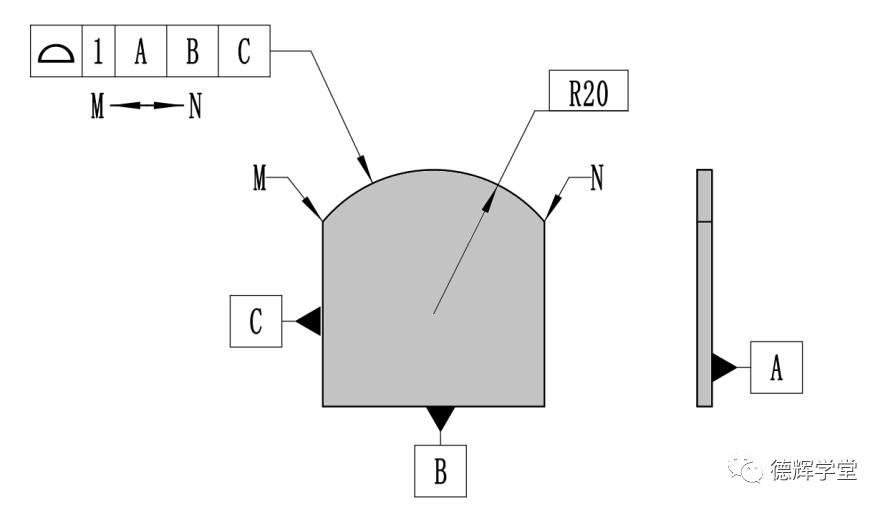
图15 图纸标注

在评价被测轮廓的轮廓度误差时，实际的操作是在被测表面上采多个点，然后评价这些点相对于理论轮廓上的理论点在矢量方向上的偏差，也就是T值。

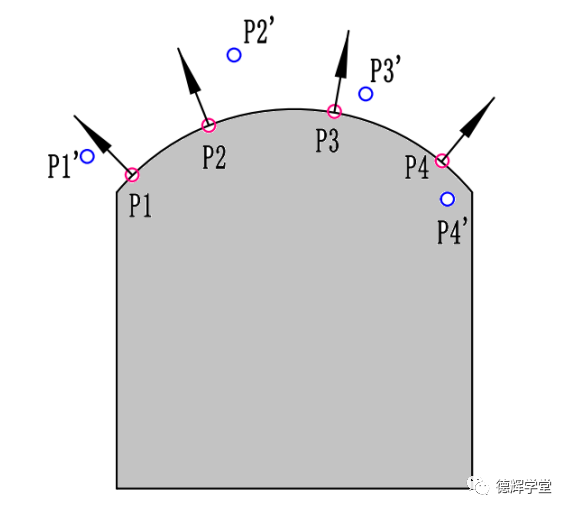
图16 实际点和理论点

图16中，已知采了4个点，理论点是P1, P2, P3, P4, 对应的实际点是P1’, P2’, P3’,P4’, 我们该怎么来计算轮廓度误差呢？很简单，我们只要计算每个实际P’点相对于理论点P在单位矢量方向上的误差即可。和T值的计算一样，见图17。

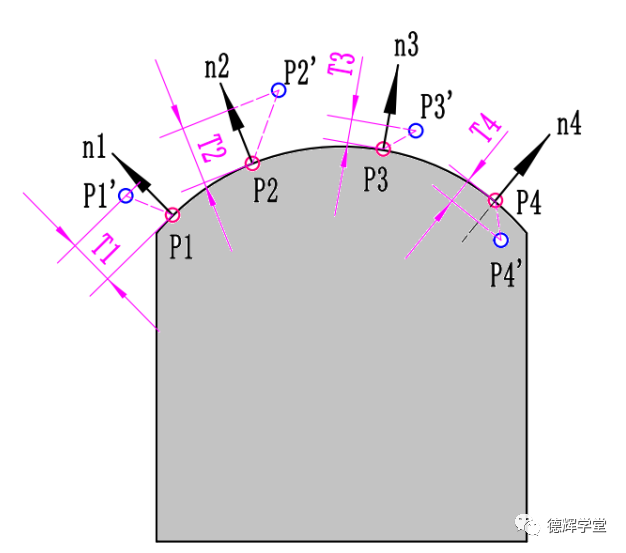
图17 轮廓度的计算原理

只要我们根据前面讲的公式（10），即T=（x2-x1）*a +（y2-y1）*b +（z2 - z1）*c分别计算出图17中的T1, T2 T3, T4, 就可以得出轮廓度的实际测量值。

注意，作为轮廓度正式输出的测量结果（即轮廓度的几何误差），ISO和ASME的要求是不同的，所以我们分两种标准讨论：

1. 如果是ISO标准，将T1-T4中的最大值乘以2就是轮廓度的实际测量值。所以图17中的轮廓度误差t：

t = 2 * T2（因为T2最大）。

只要满足t≤1则轮廓度合格。

2. 如果是ASME标准，需要给出加材料方向的最大T值和减材料方向的最大T值作为输出结果，分别为d+和d-。就图17而言:

d+ = T2

d- = T4

只要满足d+ ≤ 0.5 且 d- ≤ 0.5即合格。

     好了，我们已经知道轮廓度测量值的计算方法了，我们还是用PC-DMIS来验证一下，看看结果如何。

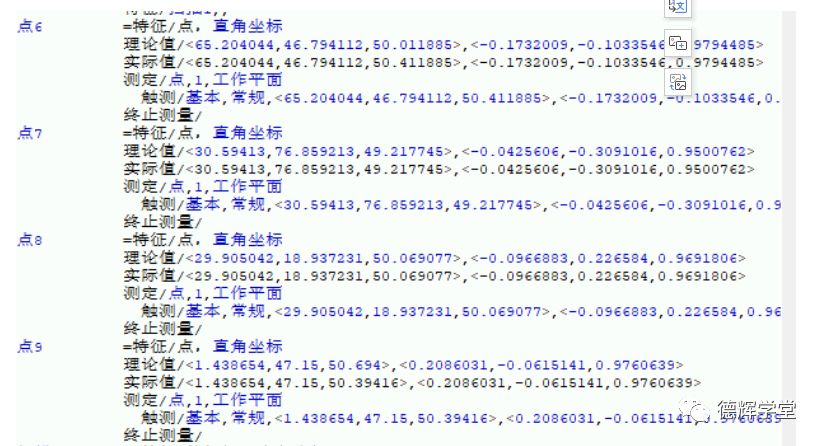
图18 理论点坐标和实际点坐标

图19 ASME的评价结果（绿框部分）

图20 ISO的评价结果（绿框部分）

我们再用手工计算来验证一下。

将图18中的数据输入做好的Excel表格，再来看看基于公式（10）做的Excel的计算结果：

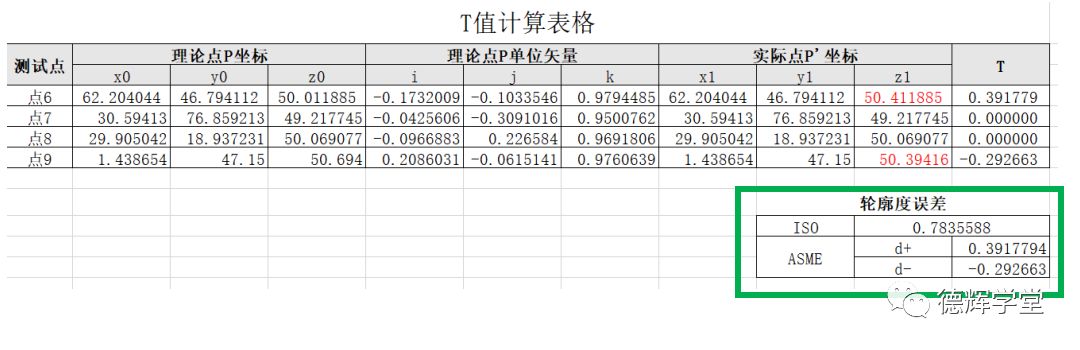
图21 基于公式计算的结果

将PC-DMIS计算的图19和图20的计算结果，与图21的结果进行比较，我们发现结果是相同的。

说明PC-DMIS采用的方法和Excel采用的方法是相同的。同样蔡司软件Calypso也是采用相同的方法。

好了，到此为止本期的文章就结束了。

可能有小伙伴还会问，你举的轮廓度例子是带基准的，如果不带基准它又是如何评价的呢？

不带基准的轮廓度其实也是计算T值，不过计算方法就比本期文章中的计算方法复杂很多，因为不带基准的轮廓度仅仅控制形状，即理想要素的形状是一定的，但理想要素的方向和位置是不确定的，需要有一个最佳拟合的过程来确定理想要素的方位。

在计算T值的时候还要引入6个参数，分别是沿x,y,z轴平移的三个参数Tx, Ty, Tz和绕x,y,z轴旋转的三个参数Rx, Ry, Rz, 通过最佳拟合的条件（比如最大值最小或最小二乘法）确定6个参数的大小，最后再确定图21中每个点T值的大小。

根据解释的难以程度，我们争取后边再来讨论不带基准轮廓度的计算原理。

最后还要补充一点，无论是海克斯康的PC-DMIS还是蔡司Calypso的轮廓度误差均采用T值来计算，注意，它其实是一种近似的做法！如果严格按照理论来做的话，应该采用下面的方法。

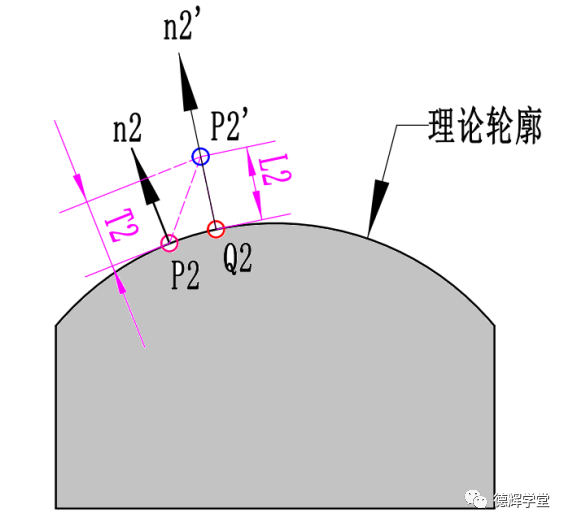
图22 计算轮廓度误差的正确方法

假设我们在实际零件上采了一点P2’，我们认为该点P2’在理论轮廓上对应的点应该是P2, 所以两者之间的偏差就是T2，这其实是有点勉强的。无论是根据ISO规定的最小区域法还是ASME Y14.5.1M中规定，要在理论轮廓上寻找真正P2’对应的理论点，该点必须满足两个条件：

1. 该点必须在理论轮廓上；

2. 该点处的单位矢量必须刚好经过实际点P2’。

比如说图22中的理论点Q2（可以证明，该点一定存在）, 该点在理论轮廓上，且该点处的单位矢量n2’刚好通过实际点P2’, 然后线段Q2P2的长度L2就是实际点相对于理论轮廓的偏置量。

也就是说，轮廓度误差计算的真正结果，应该采用图22中的L2, 而不应该采用T2.

当然，寻找Q2对于软件算法来讲，计算量非常大，而计算T2，非常容易。而且对于理论表面没有突变的轮廓来说，而这两者大小的差别非常微小，即：

T2≈L2

所以我们就近似的用图22中的T2来代替L2了。

给大家留一道思考题，根据我们的计算原理，假设表面有突变，或者在轮廓的拐弯处，轮廓度有没有突然变得非常离谱的现象呢，为什么？欢迎给我们留言发表您的看法！

本文小结

本片文章非常啰嗦，第一章花了大量的篇幅讲解解析几何的几个基本的概念。（如果要讲不带基准轮廓度的计算，还必须提矩阵的算法...）。第二章讲解了T值的计算原理，T值实际上就是矢量方向上的综合偏差。第三章讲解了轮廓度误差的计算原理，实际上就是T值的延伸，多个T值的计算，取其最大值处理成为测量结果。

最后，关于T值和轮廓度的探讨，来源于和很多网友的讨论。这里要特别感谢长春一汽的测量专家胖姐李工给予的支持，毫无保留的将她知道的T值计算方法告诉我，也要感谢测量专家神无月任工给予的支持，帮我验证蔡司轮廓度的计算原理。在写文章的过程中，群里很多其他小伙伴也零零碎碎给予了很多帮助，这里一并表示感谢。

     觉得文章不错？点个赞吧。 有不同看法？欢迎给我们留言！